Quesiti di Teoria dei fenomeni aleatori

1) Le definizioni di probabilità ed i loro legami statistici :

Ci sono 4 possibili definizioni per la probabilità :

a)    Assiomatica

La probabilità della evento certo è unitaria.

La probabilità è un numero compreso tra 0 ed 1.

La probabilità di un evento che è somma di due eventi non aventi elementi in comune è la somma delle probabilità.

b)    Frequenza di ripetizione

La frequenza relativa di un evento A è il rapporto tra il numero di prove in cui si ha come risultato un elemento della insieme A ed il numero di prove, quando quest´ultimo tende ad ¥ , la frequenza relativa tende alla probabilità.

c)    Classica

La probabilità di un evento A è il rapporto tra il numero dei possibili risultati favorevoli all´evento A ed il numero totale dei possibili risultati. Un miglioramento della definizione richiede che i singoli risultati siano equiprobabili.

d)    Soggettiva, la probabilità è il prezzo che un individuo ritiene equo pagare per ricevere 1 se l´evento si verifica.

2) Il paradosso di Bertrand :

È un paradosso legato alla definizione classica di probabilità e che la mette in crisi quando il numero dei possibili risultati è illimitato. Si abbia una circonferenza C di raggio r, si deve valutare la probabilità che una corda AB selezionata a caso abbia dimensioni maggiori del lato del triangolo equilatero inscritto nella circonferenza, si troveranno quindi almeno tre diversi risultati tutti giusti :

 

a)    Si considerino le sole corde aventi il centro all´interno del cerchio di raggio , la probabilità in termini classici può allora essere espressa come il rapporto tra 2 aree, la area del cerchio in cui può cadere il centro della corda e la area di C, la probabilità richiesta vale ¼ .

b)    Si fissi un estremo della corda, si troverà che la altro estremo deve essere compreso entro un angolo pari a 1/3 del perimetro della circonferenza, quindi la probabilità in questo caso è 1/3.

c)    Le corde più lunghe si immaginano orizzontali e con ordinata compresa tra   e   , in questo caso si trova che la probabilità vale ½ .

 

3) Teoremi della probabilità totale e di Bayes :

Il Teorema della probabilità totale afferma che se si ha una partizione dello spazio campione S in m eventi A₁ ,..., A_m ed un evento B definito su S allora la probabilità di B è data dalla relazione  , si dimostra scrivendo B come intersezione con lo spazio campionario e quindi con la partizione A₁ ,..., A_m , scomponendo e poi utilizzando la probabilità condizionata .

Il Teorema di Bayes consente per mezzo del teorema della probabilità totale di ricavare la probabilità a posteriori di un evento appartenente ad una partizione A₁ ,..., A_m di S conoscendo la sua probabilità a priori, ossia si ha . Si ricava dall´uguaglianza che scaturisce dalla probabilità condizionata ed utilizzando al denominatore il teorema della probabilità totale.

 

4) Indipendenza statistica di eventi e di variabili aleatorie :

Due eventi sono detti statisticamente indipendenti se la probabilità della evento intersezione è pari al prodotto delle probabilità dei singoli eventi . Due variabili aleatorie invece sono statisticamente indipendenti se dati due insieme arbitrari A e B di valori di X e di Y rispettivamente, si ha P{X Î A, Y Î B}= P{X Î A} P{Y Î B}.

 

5) La probabilità condizionata : Definizione ed interpretazione in termini di frequenza relativa e sue proprietà  :

È la probabilità che si verifichi un evento A dopo che si sia verificato l´evento B           . In termini di frequenza relativa, la probabilità condizionata di A dato B è approssimativamente uguale alla frequenza relativa con cui si presenta l´evento A nella successione di prove in cui si presenta l´evento B.

 

6) Prove ripetute e legge Binomiale :

Si tratta di prove che generano uno spazio campione pari al prodotto cartesiano di n spazi campione S essendo n il numero di prove ed S lo spazio campionario degli esiti della singola prova. Le prove Bernoulliane sono invece un caso particolare delle prove ripetute, in quanto le prove sono tra di loro indipendenti e ci sono solo 2 risultati possibili. Si parla invece di prove Bernoulliane generalizzate se ogni prova ha r possibili risultati.

La distribuzione dei successi è descritta dalla legge binomiale, in particolare il numero dei successi in un qualsiasi ordine è    mentre il numero dei successi in un qualsiasi ordine è .

 

7) Si definisca la funzione di distribuzione e se ne mostrino le proprietà :

La funzione di distribuzione è atta a descrivere la probabilità che un evento si verifichi sia compresa in un dato intervallo, essa è descritta dalla terminologia  quindi la funzione di distribuzione di un certo valore x della variabile aleatoria X individua la probabilità che X abbia valore inferiore ad x. Ha le seguenti proprietà :

a)    è compresa tra 0 ed 1 dovendo rappresentare una probabilità.

b)    possiede delle discontinuità di salto le quali sono continue solo da destra ed il cui valore è pari alla probabilità che la variabile aleatoria X assuma il valore x in questione .

c)                                                   

d)    Se x₁ < x₂  allora

e)    è una funzione monotona crescente.

f)    

 

8) Si scrivano e si dimostrino le proprietà della densità di probabilità :

La densità di probabilità è definita come la derivata rispetto alla variabile aleatoria X della funzione di distribuzione   , pertanto integrandola tra 2 punti x₁ ed x₂ si ottiene la probabilità che la X sia compresa in quell´intervallo ; da ciò segue che l´integrale esteso a tutto la asse reale deve valere 1.

 

9) La densità di probabilità empirica (istogramma) e la sua interpretazione in termini di frequenza relativa :

Si suddivide la asse x in intervalli di ampiezza D, dopodiché si esegue un esperimento n volte e si associa ad ogni intervallo D un gradino di altezza proporzionale al numero dei risultati che cadono nell´intervallo, si ottiene così un istogramma che deve essere normalizzato in modo che la area da esso sottesa sia unitaria ; esso tende alla funzione di distribuzione per

n ®¥ e D®0 .

 

10) Le disuguaglianze di Chebyschev e di Markov : dimostrazioni e possibili applicazioni :

Entrambe si prefiggono di limitare determinare disuguaglianze che diano un´idea su come sia distribuita la densità di probabilità.

La disuguaglianza di Chebyschev afferma che la probabilità che la variabile aleatoria X assuma valori esterni ad un intervallo arbitrario (n-e , n+e) è trascurabile se il rapporto s/e è sufficientemente piccolo :. Si ottiene impostando la soluzione come varianza di due masse di probabilità.

La disuguaglianza di Markov invece afferma che la probabilità che .

 

11) La variabile aleatoria esponenziale ed i suoi momenti di ordine 1 e 2 :

La sua densità di probabilità è data dalla . Il momento di ordine 1 si ottiene dalla   mentre il momento di ordine 2 dalla

12) La variabile aleatoria c² :

Una importante proprietà è che la somma dei quadrati di n gaussiane standard indipendenti è una c² con n gradi di libertà. È una distribuzione molto utilizzata in statistica per il calcolo della varianza di funzioni gaussiane a valor medio incognito, che si trova esser distribuita come una c² con n-1 gradi di libertà dove n in pratica coincide con la numerosità del campione.

 

13) La variabile aleatoria geometrica :

La sua densità di probabilità somiglia molto ad una binomiale a meno di un esponenziale   . Il suo valore atteso è  che si ottiene per confronto con la derivata della serie esponenziale.

 

14) La legge dei Grandi Numeri :

Essa afferma che la probabilità che la frequenza relativa differisca dalla probabilità per più di e vale 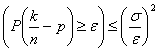 . Si dimostra semplicemente applicando la disuguaglianza di Chebyschev e ricordando che il numero dei successi è distribuito secondo una binomiale con varianza npq.

 

15) Il teorema del limite centrale ; dare uno o più enunciati ed indicare una o più applicazioni :

a)    Quando il prodotto npq®¥ la binomiale tende alla gaussiana.

b)    La convoluzione di n gaussiane è ancora una gaussiana

c)    La distribuzione della somma di n variabili aleatorie tende, al crescere di n, ad una gaussiana. Se le variabili sono continue anche la densità approssima una densità gaussiana.

d)    Se X₁ , ... , X_n  sono variabili aleatorie i.i.d. con valor medio h e varianza s² allora per n®¥ la variabile    tende ad una gaussiana standard.

 

16) L´approssimazione Poissoniana della Binomiale(Teorema di Poisson) enunciato e dimostrazione :

Nel caso di eventi rari ossia di prove ripetute per le quali la probabilità di successo sia minore del 10% , si conviene di approssimare la binomiale con la Poissoniana la cui densità di probabilità è descritta dalla  , nella quale l è il valore atteso e vale np essendo n il numero di prove e p la probabilità di successo. Il teorema si dimostra a partire dalla formula di Bernoulli  sfruttando che n >>k  ed n >>np pertanto per q = 1-p = e^-p si è potuto utilizzare lo sviluppo di Taylor valido nel caso di p infinitesimo. Sostituendo si trova  .

 

17) Il teorema fondamentale : densità di probabilità di una funzione di variabile aleatoria  :

Questo teorema consente di calcolare la densità di probabilità di una funzione di variabile aleatoria a partire dalla conoscenza della derivata della funzione e della densità di probabilità della variabile aleatoria di cui è funzione, si ha :           . Si ottiene prendendo 3 radici della equazione y=g(x) e scrivendo la  mentre quest´ultima può essere espressa agevolmente in termini della x ed infine osservando che   . Sostituendo il teorema è dimostrato.

 

18) Il concetto di indipendenza statistica tra eventi, in una coppia ed in una n-pla di variabili aleatorie :

Due variabili aleatorie sono statisticamente indipendenti se P{X £ x , Y £ y}= P{X £ x} P{Y £ y}.

 

19) Densità di probabilità di una funzione g(X,Y) di due variabili aleatorie X ed Y :

Si ottiene dalla derivata del 2° ordine della funzione di distribuzione congiunta F_XY  si ha :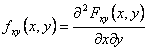

 

20) Correlazione di variabili aleatorie e coefficiente di correlazione, caso in cui l´indipendenza coincide con la scorrelazione :

Il coefficiente di correlazione di due variabili aleatorie X ed Y vale    dove m_XY  è la covarianza e vale .

Due variabili aleatorie sono dette scorrelate se E[XY] = E[X]E[Y] , relazione che sostituita nella covarianza mostra che per variabili scorrelate la covarianza ed il coefficiente di correlazione sono nulli .

Due variabili aleatorie sono dette indipendenti Û f_XY = f_X(x)f_Y(y) .

Si noti che la scorrelazione indica la assenza di un legame lineare tra le due variabili mentre l´indipendenza indica la assenza di qualsiasi tipo di legame tra le due variabili, pertanto indipendenza implica scorrelazione ma non viceversa tranne che nel caso di variabili aleatorie gaussiane.

 

21) Trasformazione di una coppia di variabili aleatorie ; dimostrare il teorema fondamentale e descrivere l´uso della variabile ausiliaria per ottenere la funzione di densità di una funzione di 2 variabili aleatorie :

Se si hanno 2 funzioni di variabili aleatorie Z e W tali che Z = f(X,Y)   e   W = g(X,Y)  allora il teorema fondamentale descrive come ottenere per mezzo del Jacobiano la funzione di densità di probabilità congiunta. Si ha    , mediante opportuna scelta di una variabile ausiliaria si può calcolare ad esempio la densità di probabilità della somma di 2 variabili aleatorie.

 

22) Parlare delle trasformazioni lineari di un vettore aleatorio e della multivariata gaussiana :

Un vettore aleatorio è un vettore tale che una qualsiasi combinazione delle sue componenti determina una variabile aleatoria gaussiana.

 

23) Ricavare la trasformazione lineare che permette di rendere incorrelate le componenti di un vettore aleatorio gaussiano a valor medio nullo e con assegnata matrice di covarianza :

 

24) La curva di regressione di una variabile aleatoria su di un´altra : proprietà generali, caso particolare di una coppia di variabili aleatorie congiuntamente gaussiane :

Si tratta della integrale che definisce il valore atteso di Y condizionato ad X  pensato come funzione di j(x).

 

25) Vita di un sistema ; affidabilità ; frequenza condizionata dei guasti e suoi andamenti tipici ; interpretazione in termini di frequenza relativa  :

La vita di un sistema è l´intervallo di tempo che intercorre tra la messa in funzione e la prima rottura, essa è descritta dalla variabile aleatoria X, la sua funzione di distribuzione F_X(t) è la probabilità che il sistema si guasti prima della istante t mentre l´inverso   è la probabilità che il sistema funzioni all´istante t ed è chiamata affidabilità.

 Il valore atteso della vita del sistema è chiamato MTBF ed individua appunto il tempo medio di funzionamento senza guasti di un sistema. Viene infine descritta la   detta frequenza condizionata dei guasti, condizionata appunto al fatto che il sistema abbia funzionato sino al tempo t. I possibili andamenti della frequenza condizionata dei guasti sono : costante, con mortalità infantile, con usura, a vasca da bagno.

 

26) Legame tra frequenza condizionata dei guasti e affidabilità ; valore atteso del tasso dei guasti  :

  detta frequenza condizionata dei guasti, condizionata appunto al fatto che il sistema abbia funzionato sino al tempo t. Il valore atteso della vita di un sistema è pari alla somma delle singole affidabilità dei sottosistemi di cui si compone.

 

27) Densità di probabilità della bivariata gaussiana e sua densità condizionata  :

 

28) Il concetto di campione aleatorio ; definizione della media di campione ; valore atteso e varianza della media di campione  :

Un campione aleatorio è un insieme di n variabili i.i.d. estratte da una unica variabile aleatoria X, la media di campione o media campionaria è descritta dalla relazione 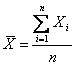 , il suo valore atteso coincide col valore atteso h della popolazione mentre la sua varianza con la varianza della popolazione ma divisa per n.

 

29) La densità di probabilità della somma di 2 variabili aleatorie nel caso generale e nel caso di indipendenza.   :

Nel caso di indipendenza essa è data dalla convoluzione delle 2 funzioni di densità delle due variabili aleatorie mentre la funzione caratteristica è pari al prodotto delle due funzioni caratteristiche.

 

30) Convergenza in media quadratica e convergenza in probabilità : definizioni e collegamento tra le due convergenze  :

La convergenza in media quadratica è data dalla relazione  .

La convergenza in probabilità invece è data dalla relazione    .

La relazione tra le due è che se X_n converge a c in media quadratica allora converge a c in probabilità come si ottiene applicando la disuguaglianza di Markov.

31) La variabile aleatoria c² : definizione ed utilizzazione statistica  :

Le proprietà della c² sono le seguenti :

a)    Se X è una c² con m gradi di libertà allora Z = X + Y  è una c² con m+n gradi di libertà.

b)    La somma dei quadrati di n gaussiane standard indipendenti è una c² con n gradi di libertà.

c)    Una c² con 2 gradi di libertà è una densità esponenziale.

 

32) Distribuzione della media e della varianza campionaria  :

La media campionaria è 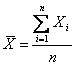 essa ha valore atteso h uguale a quello della popolazione e varianza . La varianza campionaria è , il suo valore atteso risulta esser pari alla varianza della popolazione  . Un risultato importante è che la variabile aleatoria  è distribuita come una c² con n-1 gradi di libertà. Per valori elevati di n la media campionaria segue approssimativamente la legge normale.

 

33) Decisione binaria con singola osservazione : concetti generali e test di Neyman - Pearson, quest´ultimo con relativa dimostrazione  :

Si ha una decisione binaria quando nello spazio dei segnali S ci sono 2 segnali, ad ognuno di essi è associata una delle 2 partizioni dello spazio delle osservazioni Z e deve esser presa una delle 2 decisioni d₀ o d₁ . L´errore di 1° tipo è la probabilità che il segnale fosse S₀ ma venga erroneamente presa la decisione d₁ , è indicato con a ed è detto livello di significatività del test. L´errore di 2° tipo è la probabilità che il segnale fosse S₁ ma venga erroneamente presa la decisione d₀ , è indicata con b ed il suo inverso P = 1 - b è detta potenza del test.

34) Teoria della decisione e criterio di Neyman - Pearson  :

Si propone di ripartire lo spazio delle osservazioni in modo da associarne gli elementi allo spazio delle decisioni. Il criterio di Neyman Pearson conduce alla individuazione di una regola di decisione che minimizza b avendo fissato a. In sostanza si applica il metodo dei moltiplicatori di Lagrange cercando tra tutte le regioni per le quali il livello di significatività del test è quello fissato a₀ , quella che massimizza la potenza del test b . Si trova che il rapporto di verosimiglianza è maggiore del moltiplicatore l si sceglie d₁ altrimenti si sceglie d₀.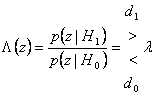   

 

35) Teoria assiomatica : Si illustri la differenza tra la stima di Bayes e quella non di Bayes ; si esemplifichi al caso di misure affette da errori  :

Nella approccio classico il parametro q della distribuzione f_X(x,q) è visto come una costante, incognita ma deterministica . Nella statistica di Bayes il parametro incognito q è visto come una realizzazione di una variabile aleatoria F .

36) Generazione di numeri pseudo - casuali con assegnata distribuzione partendo da numeri pseudo - casuali uniformi in [0,1]  :

Se X è una variabile aleatoria con distribuzione F(x) allora U = F(x) è distribuita uniformemente in (0,1) con distribuzione F(x) basta quindi applicare la F^-1(u) ad ogni u appartenente alla sequenza di numeri casuali con distribuzione uniforme in (0,1).

 

37) Descrivere il metodo Monte Carlo  :

È un metodo basato su un campionamento casuale, in sostanza si ripete n volte un esperimento aleatorio e si calcola la media dei risultati ottenuti. Il metodo è utilizzato sia per applicazioni statistiche che per applicazioni deterministiche. È utilizzato ad esempio nel calcolo di integrali per il quale sono disponibili i due seguenti metodi :

a)    Tramite riscalamenti si fa in modo di integrare tra 0 ed 1. L´integrale risulta essere il valore atteso della funzione g applicata ad una variabile uniforme in (0,1) estraendo quindi alcuni campioni, l´integrale è individuato dalla loro media campionaria.

b)    Si generano 2 variabili uniformi in (0,1) u e v  e per ogni valore della u si controlla se v è minore di g(u). L´integrale incognito è quindi dato dal rapporto tra il numero di prove in cui v_i £ g(u_i) ed il numero di prove.

 

38) Costruzione di stimatori con il metodo dei momenti  :

Il metodo dei momenti consiste nell´eguagliare i momenti della funzione di distribuzione nota con i momenti stimati

 

39) Stima di parametro con il metodo della massima verosimiglianza. Proprietà degli stimatori di massima verosimiglianza  :

Il metodo della massima verosimiglianza si basa sul prendere quel valore di q che più verosimilmente ha dato luogo ai dati osservati. Ciò in sostanza avviene derivando rispetto al parametro incognito la funzione di verosimiglianza ossia la densità del vettore aleatorio dei campioni f(x , q) pensata come funzione di q. Sono stimatori che per piccolo campioni hanno prestazioni scarse, risultano infatti polarizzati ed aventi varianza grande, con la aumentare del numero dei campioni decrescono sia la polarizzazione che la varianza e la funzione di distribuzione tende alla gaussiana.

 

40) La statistica di Pearson ed il test della bontà di adattamento tra una legge teorica ed una legge empirica  :

Il test ha lo scopo di stabilire se un dato modello teorico si adatta ai dati effettivamente rilevati, oppure se due insiemi di dati sperimentali possono essere descritti dallo stesso modello. L´ipotesi di base è che le probabilità di m eventi A_i siano uguali ad m valori dati p_0i . La statistica che si utilizza è 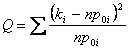 ottenuta considerando che la binomiale può essere approssimata da una normale.

41) La statistica di Pearson ed il test del c² :

La statistica del test di Pearson 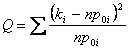 male si presta alla individuazione del percentile q_1-a allora per valori elevati di n la distribuzione della statistica viene approssimata con una c² con m-1 gradi di libertà dato che si impone il vincolo  , l´ipotesi di base viene respinta se il valore della statistica 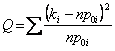 è maggiore del percentile c²_1-a(m-1).

 

42) Il metodo dei minimi quadrati : interpretazione deterministica, statistica e predittiva.  :

Si deve individuare una funzione j(x) che meglio si adatta secondo un criterio predefinito ad un insieme di punti dati. Il metodo consiste nel determinare gli m parametri l_i del modello j(x) in modo che risulti minimo l´errore quadratico .

Interpretazione deterministica :

Le coppie (x_i , y_i) sono coppie di numeri noti. Supponendo di approssimare con una retta y=a+bx_i per determinare a e b non si deve far altro che minimizzare l´errore quadratico il che si ottiene uguagliando a 0 le derivate rispetto ad a e rispetto a b.

Interpretazione statistica :

Le ascisse x_i sono numeri noti, mentre le ordinate y_i sono i valori osservati di n variabili aleatorie Y_i di valore atteso E[Y_i] = j(x_i).

Interpretazione predittiva :

Sia le ascisse che le ordinate sono i valori osservati di variabili aleatorie.