Teoria delle funzioni di una variabile complessa
1) Successione convergente :
La successione {zn} si dice convergente al limite z se " e > 0 $ un indice N(e) a partire dal quale tutti gli elementi zn della successione soddisfano la disuguaglianza |z - zn| < e per n > N(e).
2) Condizione necessaria e sufficiente affinché {zn} converga è che convergano simultaneamente {an} e {bn}:
3) Successione limitata :
Una successione è limitata se $ un numero positivo M tale che " elemento zn Î {zn} vale la disuguaglianza |zn| < M
4) Da ogni successione limitata si può estrarre una sottosuccessione convergente :
Se {zn} è limitata allora lo sono anche SRe zn e SIm zn pertanto scegliendo un opportuno nk si ha che Re znk + Im znk converge.
5) Criterio di Cauchy :
La successione {zn} è convergente Û " e > 0 si può trovare un indice N(e) tale che |zn - zm| < e per n,m ³N(e)
Þ Se zn è convergente, per il 2) debbono convergere anche le successioni reali an e bn e pertanto si può su di esse applicare il criterio di Cauchy e dire che " e > 0 $ N1(e) tale che " n ,m > N1(e) si ha che |an - am| < e / 2 e che
" e > 0 $ N2(e) tale che " n ,m > N2(e) si ha che |bn - bm| < e / 2 . Scegliendo N(e) = max( N1(e) , N2(e) ) si ha che per gli n, m maggiori di N(e) si ha |zn - zm| < e .
Ü Si può osservare che il modulo |zn - zm| è sicuramente maggiore del modulo della differenza delle parti reali oppure del modulo della differenza delle parti immaginarie, pertanto si ha |an - am| < e e |bn - bm| < e e dunque {an} e {am} sono successioni convergenti e pertanto anche {zn}.
6) Successione indefinitamente crescente :
Una successione {zn} si dice indefinitamente crescente se " numero positivo R esiste un indice N a partire dal quale i termini della successione soddisfano la condizione |zn| > R per n ³ N.
7) Punto all´infinito :
È il punto cui converge ogni successione indefinitamente crescente.
8) Definizione di punto all´infinito mediante la proiezione stereografica :
Si immagini che il piano complesso corrisponda con il piano xy di R3 e si consideri la circonferenza di raggio unitario centrata nell´origine, ebbene la trasformazione T associa ad ogni punto del piano complesso il punto della sfera che risulta dalla intersezione della sfera stessa con la congiungente del punto con il polo nord, tale intersezione risulta nel polo nord se il punto è esterno alla sfera mentre è nel polo sud se il punto è interno alla sfera, ebbene se abbiamo una successione di punti che sulla sfera tende al polo nord, allora la trasformazione inversa T-1 tende al punto all´infinito.
9) Punto interno :
Un punto z si dice punto interno della insieme E se esiste un suo intorno completamente contenuto nell´insieme E
10) Insieme aperto :
È un insieme costituito da soli punti interni.
11) Insieme connesso :
È un insieme in cui presi 2 qualsiasi punti ad esso appartenenti , essi si possono unire mediante una poligonale i cui punti sono contenuti nell´insieme stesso.
12) Dominio :
Si tratta di un insieme aperto e connesso.
13) Punto di frontiera :
Un punto z si dice punto di frontiera per E se in ogni suo intorno vi sono sia punti della insieme E che del suo complementare.
14) Dominio chiuso :
Si tratta della unione di un dominio con i suoi punti di frontiera.
15) Dominio limitato :
Si tratta di un dominio situato completamente all´interno di una circonferenza di raggio finito.
16) Limite di una funzione complessa :
Il numero w0 si dice valore limite della funzione f(z) nel punto z0 se " e > 0 si può trovare un d > 0 tale che per tutti i punti z che soddisfano la condizione 0 < | z - z0 | < d vale la disuguaglianza |f(z) - w0| < e .
17) Continuità di una funzione complessa :
La funzione f(z) è continua nel punto z0 se " e > 0 si può trovare un d > 0 tale che per tutti i punti z che soddisfano la condizione | z - z0 | < d vale la disuguaglianza |f(z) - f(z0)| < e .
18) Derivata di funzione di una variabile complessa :
Se esiste finito il limite ![]() allora questo limite si dice derivata della funzione f(z) rispetto alla variabile complessa z nel punto z0 .
allora questo limite si dice derivata della funzione f(z) rispetto alla variabile complessa z nel punto z0 .
19) Interpretazione geometrica della derivata complessa :
Anche nel caso complesso la derivata è vista come rapporto tra la variazione nell´immagine Dw e la variazione nel dominio Dz , al limite per quest´ultima che tende a 0, non curandoci del fatto che sia il dominio che l´immagine sono bidimensionali, si ha quindi ![]() si tratta cioè di un numero complesso il cui argomento a è dato dalla differenza tra la argomento del numeratore e la argomento del denominatore ma questi argomenti quando Dz®0 sono pari alle tangenti alle rispettive curve nell´immagine e nel dominio e cioè sono pari alla angolo compreso tra la asse reale e il vettore Dz o Dw
si tratta cioè di un numero complesso il cui argomento a è dato dalla differenza tra la argomento del numeratore e la argomento del denominatore ma questi argomenti quando Dz®0 sono pari alle tangenti alle rispettive curve nell´immagine e nel dominio e cioè sono pari alla angolo compreso tra la asse reale e il vettore Dz o Dw ![]() questa differenza è la stessa per ogni altro punto passante per z0 . Questa proprietà è detta di conservazione degli angoli.
questa differenza è la stessa per ogni altro punto passante per z0 . Questa proprietà è detta di conservazione degli angoli.
La proprietà della dilatazione lineare, si ottiene invece facendo il modulo della ![]() da cui si trova che
da cui si trova che ![]() e quindi k individua il coefficiente di scala della similitudine.
e quindi k individua il coefficiente di scala della similitudine.
20) Definizione di funzione differenziabile in senso complesso :
f(z) è differenziabile in z0 se rispetta la seguente equazione:
![]()
essendo ![]() e
e ![]() .
.
21) f è analitica in z0 Û f è differenziabile in z0 e si ha ![]() :
:
Þ Deriva direttamente dalla definizione di funzione analitica
Ü Basta prendere la definizione di differenziabilità ![]()
portare f(z0) al primo membro e dividere per (z-z0) sfruttando poi che ![]() si ha la definizione di derivabilità la quale si ha solo nel caso che f sia analitica.
si ha la definizione di derivabilità la quale si ha solo nel caso che f sia analitica.
22)Se la funzione f(z) = u(x, y) + i v(x, y) è derivabile nel punto z0 = x0 + iy0 allora nel punto (x0 , y0) esistono le derivate parziali delle funzioni u(x, y) e v(x, y) rispetto alle variabili x ed y e sussiste la relazione di Cauchy -Riemann
a) ux = vy b) uy = -vx
Per definizione una funzione è analitica se è differenziabile ed ![]() ma del resto si ha che
ma del resto si ha che ![]() quindi
quindi ![]() ed analogamente
ed analogamente ![]() sostituendo nella precedente si ottengono proprio le condizioni di Cauchy-Riemann.
sostituendo nella precedente si ottengono proprio le condizioni di Cauchy-Riemann.
23) Funzione analitica o olomorfa o regolare :
La funzione f(z) si dice analitica, olomorfa o regolare se è derivabile in tutti i punti del dominio e la sua derivata è continua.
24) f è analitica Û le derivate parziali delle funzioni u(x, y) e v(x, y) esistono, sono continue e per esse valgono le condizioni di Cauchy - Riemann :
25) Teorema di Gouisal :
Se f è analitica su di un insieme aperto allora f Î C´
26) Funzione intera :
Si tratta di una funzione olomorfa in tutto C .
27) Applicazione conforme :
Si tratta della trasformazione di un intorno del punto z0 nell´intorno del punto w0 effettuata dalla funzione analitica
w = f(z), avente nel punto z0 la proprietà di conservazione degli angoli e di costanza della dilatazione lineare.
28) Forma differenziale lineare :
w = A(x, y)dx + B(x, y) dy A, B complesse continue su W .
29) Teorema di Gauss - Green :
Sia W aperto (limitato) e ¶W regolare a tratti tale che w Î C´(W) Ç C(W)
![]()
30) Forma differenziale chiusa :
Una forma differenziale w si dice chiusa se è esatta e derivabile , per una forma differenziale chiusa si ha Ay = Bx .
31) Se W è un dominio semplicemente connesso, Þ
w è chiusa Û w è esatta
Þ Se w è chiusa allora Rot F = 0 cioè Ay = Bx pertanto applicando il teorema di Gauss Green al contrario si ha ![]() e quest´ultima è una delle definizioni di w esatta ossia che il suo integrale lungo un percorso chiuso sia nullo.
e quest´ultima è una delle definizioni di w esatta ossia che il suo integrale lungo un percorso chiuso sia nullo.
Ü Se w è esatta allora ammette una funzione potenziale U tale che A = Ux e B=Uy derivando la prima rispetto ad y e la seconda rispetto ad x e sfruttando il teorema di Schwarz sull´uguaglianza delle derivate miste, si ha
Ay = Uxy = Uyx = Bx e pertanto si ha che w è chiusa.
32) Formula di Green nel caso complesso :
![]()
Essendo ![]() si ha che
si ha che![]() con A=f e B= if quindi si ha a partire dal risultato valido nel campo reale
con A=f e B= if quindi si ha a partire dal risultato valido nel campo reale ![]()
33) Contorno chiuso :
Si tratta di una curva chiusa regolare a tratti priva di auto intersezioni.
34) Teorema di Cauchy :
In un dominio semplicemente connesso sia definita una funzione analitica f(z) Þ l´integrale di f(z) esteso ad ogni contorno chiuso G, completamente contenuto nel dominio G, è uguale a 0.
![]() avendo applicato le condizioni di Cauchy Riemann dato che f è analitica.
avendo applicato le condizioni di Cauchy Riemann dato che f è analitica.
35) Seconda formulazione del teorema di Cauchy :
Se la funzione f(z) è analitica in un dominio semplicemente connesso limitato da un contorno regolare a tratti C ed è continua nel dominio chiuso G Þ l´integrale della funzione f(z) esteso alla frontiera del dominio G è uguale a zero.
36) Integrali di Fresnel :
Integrando ![]() su di un circuito chiuso , si ottengono i 2 integrali reali
su di un circuito chiuso , si ottengono i 2 integrali reali ![]()
37) Formula integrale di Cauchy :
Se f(z) è analitica dentro e lungo la frontiera C di una regione semplicemente connessa R Þ![]()
Si noti infatti che f(z) è analitica ovunque eccetto che in z = a , quindi l´integrale è indipendente dal circuito chiuso che racchiude a , ossia l´integrale lungo C è uguale all´integrale effettuato lungo una circonferenza di raggio e centrata in a ossia ![]() , una parametrizzazione per G è z = a + e ei q e quindi dz = i e ei q sostituendo si ottiene
, una parametrizzazione per G è z = a + e ei q e quindi dz = i e ei q sostituendo si ottiene
![]() e passando al limite per e ® 0 ed isolando f(a) si ottiene la tesi.
e passando al limite per e ® 0 ed isolando f(a) si ottiene la tesi.
38) Teorema del valor medio :
Sia f olomorfa nel dominio A Þ il valore di f in un punto di A è uguale alla media dei valori di f su una qualunque circonferenza centrata in quel punto e contenuta, insieme al suo interno, in A : ![]()
Si dimostra a partire dalla formula di Cauchy ![]() dove ammettendo che z = a + rei q sia una parametrizzazione del cerchio C si ha dz = irei q e sostituendo nell´integrale si ottiene
dove ammettendo che z = a + rei q sia una parametrizzazione del cerchio C si ha dz = irei q e sostituendo nell´integrale si ottiene ![]() .
.
39) Principio del massimo modulo :
Sia f(z) analitica dentro e lungo una linea semplice chiusa C Þ il massimo di |f(z)| si trova lungo C a meno che f(z) non sia una costante.
La funzione è continua su di un compatto quindi ammette un massimo, supponiamo per assurdo che tale massimo sia assunto in un punto a interno al dominio, applicando il teorema della media su di un cerchio centrato in a si avrà ![]() quindi il valore della f(a) è proprio M ed è uguale al valor medio, ma per i punti della circonferenza si ha aversi |f(a)| > |f(a+rei q)| allora non si può raggiungere il valore medio M e questo implica che era un assurdo e che quindi il massimo viene assunto sul bordo del cerchio. Evidentemente quindi se il massimo è interno al dominio, la funzione non può che essere costante all´interno dello stesso, se così non è allora la funzione assume il massimo sul bordo della insieme.
quindi il valore della f(a) è proprio M ed è uguale al valor medio, ma per i punti della circonferenza si ha aversi |f(a)| > |f(a+rei q)| allora non si può raggiungere il valore medio M e questo implica che era un assurdo e che quindi il massimo viene assunto sul bordo del cerchio. Evidentemente quindi se il massimo è interno al dominio, la funzione non può che essere costante all´interno dello stesso, se così non è allora la funzione assume il massimo sul bordo della insieme.
Abbiamo in tal modo dimostrato che la funzione è costante all´interno del cerchio di centro a, per estendere il risultato a tutto il dominio, si prende un qualsiasi punto e lo si congiunge con una linea ad a, dopodichè si prende un punto su questa linea che sia prossimo al bordo del primo cerchio e lo si assume come centro del nuovo cerchio su cui ripetere le considerazioni precedenti.
40) Corollario del Principio del massimo :
Sia A un dominio limitato ed f olomorfa in A, continua in A , e non costante Þ la funzione z® |f(z)| assume il massimo sulla frontiera di A.
41) Teorema del minimo modulo :
Sia f(z) analitica dentro e lungo la linea semplice chiusa C e sia f(z) ¹ 0 dentro C Þ |f(z)| assume il suo minimo lungo C.
f(z) è analitica dentro C e dato che non ha zeri in tale dominio segue che anche ![]() è analitica dentro C quindi essendo nelle condizioni di validità del teorema del massimo modulo tale funzione può ammettere il massimo unicamente sulla frontiera C e quindi specularmente |f(z)| può assumere il minimo unicamente sulla frontiera C.
è analitica dentro C quindi essendo nelle condizioni di validità del teorema del massimo modulo tale funzione può ammettere il massimo unicamente sulla frontiera C e quindi specularmente |f(z)| può assumere il minimo unicamente sulla frontiera C.
42) Valutazione della derivata di un integrale dipendente da un parametro :
La derivata della integrale è pari all´integrale della funzione integranda derivata rispetto al parametro.
43) Lemma di derivazione sotto il segno di integrale :
Sia A un dominio e G un arco di curva orientata, e j una funzione definita e continua su G Þ la grandezza ![]() definisce in A \ G una funzione olomorfa, e la sua derivata ha l´espressione
definisce in A \ G una funzione olomorfa, e la sua derivata ha l´espressione
![]()
inoltre f possiede derivate di ogni ordine e si ha ![]() .
.
Si parte dall´integrale di Cauchy ![]() , la funzione integranda è analitica rispetto a z e la sua derivata parziale è
, la funzione integranda è analitica rispetto a z e la sua derivata parziale è ![]() quindi ricordando che l´integrale di Cauchy è un integrale dipendente dal parametro z , si ha che la sua derivata è pari all´integrale della derivata rispetto al parametro della funzione integranda.
quindi ricordando che l´integrale di Cauchy è un integrale dipendente dal parametro z , si ha che la sua derivata è pari all´integrale della derivata rispetto al parametro della funzione integranda.
44) Teorema di Taylor :
Sia f è analitica all´interno del cerchio C con centro in a Þ la serie di Taylor di f nel punto a : ![]() converge ad f(z).
converge ad f(z).
Sia z un punto interno a C e si costruisca un cerchio C1 il quale racchiuda z ma sia contenuto in C ed entrambe i cerchi siano centrati in a . Il valore di f(z) è quindi dato dalla formula integrale di Cauchy ![]() ma del resto si ha
ma del resto si ha 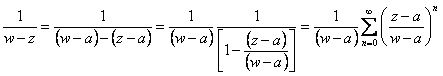 a patto che sia il rapporto minore di 1 ossia |z-a| < |w-a| quindi all´interno del cerchio C1 . A questo punto si moltiplica per f(w) / 2pi , si integra su C1 ottenendo quindi al primo membro la f(z) mentre al 2° membro
a patto che sia il rapporto minore di 1 ossia |z-a| < |w-a| quindi all´interno del cerchio C1 . A questo punto si moltiplica per f(w) / 2pi , si integra su C1 ottenendo quindi al primo membro la f(z) mentre al 2° membro 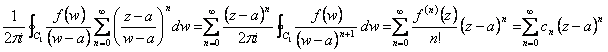
45) Unicità dello sviluppo in serie di potenze :
Sia f olomorfa nel dominio A z0 Î A ,e si abbia, in un intorno di z0 ![]() Þ
Þ ![]()
46) Disuguaglianza di Cauchy :
Se f(z) è analitica dentro e lungo il cerchio C di raggio r e centro in z = a, ![]() essendo M : |f(z)| < M
essendo M : |f(z)| < M
Si parte dalla formula integrale della derivata di Cauchy ![]() da cui prendendo il modulo e maggiorando l´integrale curvilineo con la lunghezza della circonferenza 2pr moltiplicata per il massimo M assunto dalla funzione sulla circonferenza si ottiene
da cui prendendo il modulo e maggiorando l´integrale curvilineo con la lunghezza della circonferenza 2pr moltiplicata per il massimo M assunto dalla funzione sulla circonferenza si ottiene 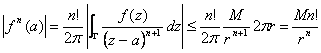 .
.
47) Teorema di Liouville :
Se per tutti i punti della intero piano complesso, f(z) è analitica e limitata Þ f(z) è costante.
Si ottiene dalla disuguaglianza di Cauchy prendendo n = 1 si ha ![]() ed essendo la derivata prima nulla " z segue che la funzione deve essere costante.
ed essendo la derivata prima nulla " z segue che la funzione deve essere costante.
48) Teorema fondamentale della algebra :
Ogni polinomio di grado n ³ 1 possiede almeno uno zero nel piano complesso.
Ammettiamo per assurdo che il polinomio P(z) non abbia zeri, quindi ![]() è analitica per qualsiasi z e risulta anche essere limitata in modulo per z® +¥ quindi per il teorema di Liouville la funzione deve essere costante, ma un polinomio non può essere costante essendo di grado n ³1 e dunque si cade in contraddizione, di conseguenza il polinomio deve ammettere almeno uno zero, si dimostrerà poi che il n° degli zeri è esattamente n.
è analitica per qualsiasi z e risulta anche essere limitata in modulo per z® +¥ quindi per il teorema di Liouville la funzione deve essere costante, ma un polinomio non può essere costante essendo di grado n ³1 e dunque si cade in contraddizione, di conseguenza il polinomio deve ammettere almeno uno zero, si dimostrerà poi che il n° degli zeri è esattamente n.
49) Teorema di Laurent :
Se f(z) è analitica dentro e lungo 2 cerchi concentrici di raggio rispettivamente R1 ed R2 e centro in a Þ
![]() con
con ![]()
DIMOSTRAZIONE DELL´ESISTENZA
Individuiamo 2 circonferenze di raggio R1 ed R2 < R1 contenute all´interno della corona circolare ed un punto z interno alle 2 circonferenze, allora il valore della funzione in questo punto z è dato dalla formula di Cauchy , ![]() per il 1° termine si ragiona così come per la serie di Taylor individuando la somma di una serie convergente
per il 1° termine si ragiona così come per la serie di Taylor individuando la somma di una serie convergente 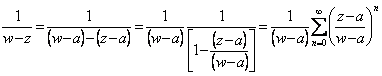 pertanto si ha
pertanto si ha ![]() con
con ![]() .
.
Raccogliendo analogamente per il 2° membro 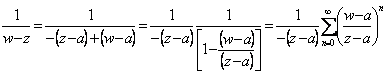 si ottiene
si ottiene ![]() con
con ![]() . Dato che all´interno della corona circolare la funzione è analitica, Þ si può applicare il teorema di Cauchy e quindi l´integrale è indipendente dal particolare percorso, ne segue che le 2 soluzioni possono essere raggruppate nella
. Dato che all´interno della corona circolare la funzione è analitica, Þ si può applicare il teorema di Cauchy e quindi l´integrale è indipendente dal particolare percorso, ne segue che le 2 soluzioni possono essere raggruppate nella ![]() con
con ![]() .
.
DIMOSTRAZIONE DELL´UNICITA´
Si ipotizza di avere 2 serie che differiscono per un solo coefficiente, le si moltiplica entrambe per (z-z0)-m-1 e se ne fa l´integrale lungo una circonferenza compresa nella anello di olomorfia ed avente centro in z0 , sostituendo a questo punto z = Reiq si trova un integrale che vale 0 se n¹m mentre vale 2pi se n=m , in definitiva in ogni sviluppo c´è un solo termine non nullo ed è uguale per le due serie che quindi coincidono.
50) Singolarità eliminabile :
Se una funzione ad un sol valore non è definita in z = a, ma esiste il ![]() si dice che z = a è una singolarità eliminabile.
si dice che z = a è una singolarità eliminabile.
51) Se f(z) è analitica e limitata in un dominio che esclude z0 , allora il punto z0 è un punto singolare eliminabile :
Affinchè z0 sia un punto singolare eliminabile, i coefficienti della parte principale della serie di laurent debbono essere tutti nulli, il che si dimostra scrivendo cn in termini della integrale ed effettuando le consuete maggiorazioni tenendo conto che la funzione è limitata cioè !f(z)| < M , sostituendo poi (z – z0) = reiq e facendo il limite per r®0 si ottiene 0 come voluto.
52) Polo :
Se una funzione ad un sol valore ha un polo in z = a, Þ ![]() ed il numero di termini presenti nella parte principale della serie di Laurent corrisponde all´ordine del polo.
ed il numero di termini presenti nella parte principale della serie di Laurent corrisponde all´ordine del polo.
53) Se il punto z0 è un polo della funzione analitica f(z) Þ per z®z0 il modulo della funzione f(z) cresce infinitamente, indipendentemente dal modo in cui il punto z tende al punto z0 :
Basta scrivere lo sviluppo di Laurent a partire dal termine –m supponendo appunto un polo di ordine m, raccogliendo nella parte principale (z-z0)-m si ha ![]() dove la j(z) è analitica e limitata in un intorno di z0 e quindi il termine (z-z0)-m comanda e spinge verso infinito la f(z) per z®z0 .
dove la j(z) è analitica e limitata in un intorno di z0 e quindi il termine (z-z0)-m comanda e spinge verso infinito la f(z) per z®z0 .
54) Se una funzione f(z), analitica in un intorno di un suo punto singolare isolato z0 cresce infinitamente in modulo indipendentemente dal modo in cui il punto z tende al punto z0 Þ il punto z0 è un polo della funzione f(z) :
Si considera la funzione ![]() la quale tende a 0 per z®z0 è quindi limitata e pertanto per essa z0 è una singolarità eliminabile e si può pertanto scrivere
la quale tende a 0 per z®z0 è quindi limitata e pertanto per essa z0 è una singolarità eliminabile e si può pertanto scrivere ![]() dove j(z) è una funzione analitica tale che j(z0) ¹0 si ha quindi che
dove j(z) è una funzione analitica tale che j(z0) ¹0 si ha quindi che ![]() che è la definizione di polo di ordine m.
che è la definizione di polo di ordine m.
55) Singolarità essenziale :
Se f(z) è una funzione ad un sol valore Þ ogni singolarità che non sia ne un polo ne uno zero è una singolarità essenziale, in particolare se z = a è una singolarità essenziale allora la parte principale dello sviluppo di Laurent ha un numero infinito di termini.
56) Funzione meromorfa :
Una funzione si dice meromorfa se è analitica in tutto il piano ad eccezione di un numero finito di poli.
57) Teorema di Casorati - Weierstrass :
Per ogni e>0 in qualsiasi intorno di un punto singolare essenziale z0 della funzione f(z) esiste almeno un punto z1 in cui il valore della funzione f(z) differisce da un numero complesso B assegnato arbitrariamente per meno di e.
Supponiamo per assurdo che esista un intorno di z0 nel quale si verifichi che ![]() , allora la funzione
, allora la funzione ![]() è limitata e quindi il punto z0 è un punto singolare eliminabile della y
è limitata e quindi il punto z0 è un punto singolare eliminabile della y
che dunque per il precedente teorema, può essere scritta come ![]() e ricavando f(z) dalla
e ricavando f(z) dalla ![]() si ottiene
si ottiene ![]() ma se m=0 questo sviluppo individua un punto regolare per f(z) altrimenti individua un polo di ordine m e non una singolarità essenziale come il teorema richiedeva.
ma se m=0 questo sviluppo individua un punto regolare per f(z) altrimenti individua un polo di ordine m e non una singolarità essenziale come il teorema richiedeva.