Serie complesse
Serie Numeriche
1) Serie convergente :
La serie ![]() si dice convergente se è convergente la successione {Sn} delle sue somme parziali, in tal caso il limite S della successione {Sn} si dice somma della serie
si dice convergente se è convergente la successione {Sn} delle sue somme parziali, in tal caso il limite S della successione {Sn} si dice somma della serie ![]() .
.
2) Resto n-esimo della serie:
Si tratta della serie ![]() .
.
3) Criterio di convergenza di Cauchy :
La serie ![]() è convergente Û " e > 0 si può trovare un indice N tale che
è convergente Û " e > 0 si può trovare un indice N tale che 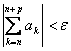 per n ³N .
per n ³N .
4) Serie assolutamente convergente :
Se la serie a termini reali ![]() allora è convergente anche la serie
allora è convergente anche la serie ![]() che in questo caso è detta assolutamente convergente.
che in questo caso è detta assolutamente convergente.
5) Criterio di convergenza di D´Alembert :
La serie ![]() è convergente se, a partire da un indice N, vale la relazione
è convergente se, a partire da un indice N, vale la relazione ![]() " n ³ N.
" n ³ N.
6) Criterio di convergenza di Cauchy :
La serie ![]() è convergente se, a partire da un indice N, vale la relazione
è convergente se, a partire da un indice N, vale la relazione ![]() " n ³ N.
" n ³ N.
Serie di funzioni
7) Convergenza puntuale :
La serie di funzioni ![]() si dice convergente nel suo dominio se la serie numerica ad essa relativa converge " z ossia se " z e per ogni numero positivo e si può trovare un indice N tale che
si dice convergente nel suo dominio se la serie numerica ad essa relativa converge " z ossia se " z e per ogni numero positivo e si può trovare un indice N tale che ![]() per n > N .
per n > N .
8) Convergenza uniforme :
La serie di funzioni ![]() si dice uniformemente convergente nel suo dominio se la serie numerica ad essa relativa converge " z ossia se " numero positivo e si può trovare un indice N(e) tale che " n > N(e) ,
si dice uniformemente convergente nel suo dominio se la serie numerica ad essa relativa converge " z ossia se " numero positivo e si può trovare un indice N(e) tale che " n > N(e) , ![]() per ogni z appartenente al dominio.
per ogni z appartenente al dominio.
9) Criterio di Weierstrass di convergenza totale:
Se in un dominio i moduli dei termini della serie di funzioni ![]() sono maggiorati ovunque dai termini di una serie numerica assolutamente convergente Þ la serie
sono maggiorati ovunque dai termini di una serie numerica assolutamente convergente Þ la serie ![]() converge uniformemente nel suo dominio.
converge uniformemente nel suo dominio.
10) Criterio di Cauchy :
Condizione necessaria e sufficiente per la convergenza uniforme della serie ![]() è che " e > 0 esista un N(e) tale che la relazione
è che " e > 0 esista un N(e) tale che la relazione ![]() sia verificata simultaneamente in tutti i punti del dominio per n ³ N e " m.
sia verificata simultaneamente in tutti i punti del dominio per n ³ N e " m.
11) Teorema di Weierstrass sulle proprietà delle serie uniformemente convergenti :
Se le funzioni un(z) sono continue in u dominio e se la serie ![]() converge uniformemente in questo dominio alla funzione f(z) Þ anche f(z) è continua nello stesso dominio .
converge uniformemente in questo dominio alla funzione f(z) Þ anche f(z) è continua nello stesso dominio .
12) Teorema di Abel o di Cauchy - Hadamard:
Se la serie di potenze ![]() converge in un punto z1 ¹ z0 , Þ essa converge assolutamente anche in un punto z tale che |z-z0| < |z1 - z0| ; inoltre la serie converge uniformemente in ogni cerchio |z-z0| £ r di raggio r < |z1 - z0|.
converge in un punto z1 ¹ z0 , Þ essa converge assolutamente anche in un punto z tale che |z-z0| < |z1 - z0| ; inoltre la serie converge uniformemente in ogni cerchio |z-z0| £ r di raggio r < |z1 - z0|.
Essendo la serie convergente in z1 allora i suoi termini tendono a zero per n®¥ pertanto il termine generale può essere maggiorato da una costante M cioè ![]() e quindi si ha
e quindi si ha ![]() ma noi siamo interessati a vedere se converge assolutamente la serie per un punto z tale che |z-z0|<|z1 - z0| quindi prendiamo il modulo della serie di potenze
ma noi siamo interessati a vedere se converge assolutamente la serie per un punto z tale che |z-z0|<|z1 - z0| quindi prendiamo il modulo della serie di potenze  ma quest´ultima è una serie geometrica di ragione q<1 e pertanto è convergente quindi per il criterio del confronto la serie data converge assolutamente. Per dimostrare la convergenza uniforme si utilizza il criterio di Weierstrass che prevede la maggiorazione con una serie numerica convergente quale ad esempio può essere
ma quest´ultima è una serie geometrica di ragione q<1 e pertanto è convergente quindi per il criterio del confronto la serie data converge assolutamente. Per dimostrare la convergenza uniforme si utilizza il criterio di Weierstrass che prevede la maggiorazione con una serie numerica convergente quale ad esempio può essere 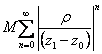 essendo r < |z1 - z0| .
essendo r < |z1 - z0| .
13) Sia ![]() una serie di potenze convergente a f(z) nel cerchio di convergenza D(z0 , R)
una serie di potenze convergente a f(z) nel cerchio di convergenza D(z0 , R)
Þ f(z) è analitica e f ´(z) = ![]()
14) Teorema del passaggio del limite sotto il segno di integrale:
Data una serie di funzioni ![]() continue e uniformemente convergente ad u(z) in un dominio D
continue e uniformemente convergente ad u(z) in un dominio D
Þ " curva G regolare a tratti contenuta in D si ha ![]()
Si osserva che la differenza tra i due integrandi è pari al resto n-esimo ed essendo la serie uniformemente convergente, esso può essere maggiorato cioè ![]() dove L è la lunghezza della curva lungo la quale si integra, pertanto si ha
dove L è la lunghezza della curva lungo la quale si integra, pertanto si ha ![]() e dunque c´è l´uguaglianza tra i due termini.
e dunque c´è l´uguaglianza tra i due termini.