Gamma, Beta, funzioni di Bessel

Funzioni di Eulero

1) Gamma di Eulero :

 si tratta di una funzione olomorfa nel piano Rez > 0 .

 

2) Formula di ricorrenza :

Si ottiene calcolando l´integrale per parti, si ha .

 

3) Formula del fattoriale :

Si ottiene dalla formula di ricorrenza     ;        sino ad arrivare alla      e ponendo in essa z = 1 si ottiene il risultato.

 

4) Estensione della G(z) anche a valori negativi di z :

Nel ricavare la  iterando la formula di ricorrenza sino a giungere alla G(z+n) si ottiene al secondo membro una espressione moltiplicata per la G(z) che quindi può essere estrinsecata, si ottiene una relazione indipendente da n come si può verificare sostituendo n = n+p , la relazione ha validità per Re(z+n) >0 e presenta n singolarità polari.

 

5) Quale relazione lega la G all´integrale di Gauss :

Si ottiene sostituendo prima t=s² nella definizione della G(z) e dopo si pone z = ½  e ci si ricorda del valore della integrale di Gauss  .

 

6) Beta di Eulero  :

 

7) Relazione tra la Beta e la Gamma di Eulero :

Si sostituisce t=u² nella G(p) e t=s² nella G(q) dopodichè si moltiplicano tra di loro raccogliendo i fattori comuni, si ottiene sostituendo nella quale u=rcosq  e  s=rsenq   con duds=rdrdq si giunge all´integrale    dove 2 moltiplicato per l´integrale è proprio la b(p,q) che si può ottenere sostituendo t=cos²q .

 

8) Formula dei complementi :

Si ottiene scrivendo la b in termini della G quindi effettuando la sostituzione  e risolvendo l´integrale che diviene l´integrale indefinito di una funzione polidroma mediante il teorema dei residui.

Funzioni di Bessel

9) Funzione generatrice delle funzioni di Bessel :

È una funzione olomorfa alla quale è associata una serie di Laurent con infiniti termini ad esponente negativo ed infiniti termini ad esponente positivo, si ha cioè 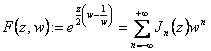 dove i coefficienti J_n di questo sviluppo sono detti funzioni di Bessel di prima specie.

 

10) Valore dei coefficienti J_n(z) :

Si ottengono a partire dalla funzione generatrice

posso moltiplicare in quanto le due serie convergono assolutamente si ha e ponendo n-m=k si ha quindi si ha .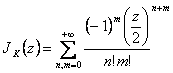

 

11) Dimostrare la formula  J_-n (z) = (-1)ⁿ J_n(z):

Si ha  .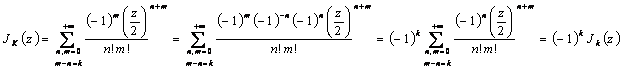

 

12) Equazione differenziale di Bessel di ordine n :

È un´equazione differenziale nella forma  la sua soluzione è la funzione di Bessel di 1ª specie di ordine n. Si ottiene derivando entrambe i membri della 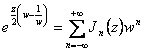  rispetto a z e rispetto a w , si ha :    da cui osservando che moltiplicando o dividendo per w si va a modificare il suo coefficiente k, si ha : e quindi si ottiene

J_{n - 1}  - J_{n +1} = 2 J´_n  .                 Derivando rispetto a w invece si ha   da cui  e quindi si ottiene .

Sommando le 2 relazioni ottenute si ha  ed incrementandola si ha , invece sottraendo le 2 relazioni si ha  e derivandola rispetto a z si ha   e sostituendo le ultime 2 nella terzultima si ottiene l´equazione differenziale di Bessel  .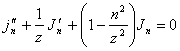

 

13) Sviluppo delle funzioni trigonometriche in serie di funzioni di Bessel :

Si ottiene ponendo nella funzione generatrice     w = e^iq   ottenendo quindi

Estrinsecando si ha

Da cui eguagliando i termini reali ed i termini immaginari e ponendo j = p/2 si ottengono i 2 seguenti sviluppi :

                                          

 

14) Applicazione della equazione differenziale di Bessel :

Una sua applicazione è nell´equazione del moto di una membrana circolare.

 

15)    Rappresentazione integrale delle funzioni di Bessel :

Considerando di poter associare alla funzione una serie di Laurent, i coefficienti c_n si calcolano con l´integrale curvilineo, tipico ad esempio del residuo, calcolando questo integrale si ottiene la seguente :

Si ottiene ricordando che i J_n(z) non sono altro che i coefficienti di una serie di laurent e questi sono dati dall´integrale 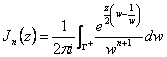   e sostituendo w=e^iq si ottiene il risultato.