Teoremi sulle successioni e sulle serie di funzioni

Successioni di funzioni

1) Criterio di Convergenza puntuale :

Condizione necessaria e sufficiente perché la successione di funzioni  f_n converga puntualmente in A è che, fissato e > 0, " tÎA esista N(e,t) tale che :                |f_n(t) - f_m(t)| < e                      " n, m > N             .

 

2) Criterio di Convergenza uniforme :

Condizione necessaria e sufficiente perché la successione di funzioni  f_n converga uniformemente in A è che, fissato e > 0, esista N(e) tale che :       |f_n(t) - f_m(t)| < e        " tÎA                  " n, m > N             .

 

3) Il limite di una successione di funzioni limitate f_n convergente uniformemente è una funzione limitata :

Si parte dalla definizione della uniforme convergenza |f_n(t) - f_m(t)| < e    se n, m > N    dopodiché si manda n ad ¥  e si pone m = N.   A questo punto si può utilizzare la disuguaglianza triangolare e scrivere |f(t)| - |f_N(t)| < |f(t) - f_N(t)| < e

Þ ponendo e = 1    si ha     |f(t)| < 1 + |f_N(t)|      e quindi il sup del |f| è limitato dal sup di |f_N|

 

4) Teorema dello scambio dei limiti

Sia  uniformemente in A   e                  Þ         

Dimostro prima che la successione l_n a destra della uguale è convergente, troveremo che il suo limite è l e lo stesso limite si avrà anche per il 1° membro. La convergenza si stabilisce in base al criterio di convergenza uniforme, infatti si ha

 |l_n - l_m|  = |l_n - f_n(t) + f_n(t) - f_m(t) + f_m(t) - l_m|  £  |l_n - f_n(t)| + |f_n(t) - f_m(t)| + |f_m(t) - l_m| < e   essendo i moduli esterni minori di e per  ed il modulo centrale minore di e per la convergenza uniforme in A.  Rimane quindi solo da dimostrare che il 1° membro     per far ciò impostiamo la consueta disuguaglianza dei limiti cioè |f(t) - l|  £  |f(t) - f_N(t)| + |f_N(t) - l_N(t)| + |l_N(t) - l|  £  2e + |f_N(t) - l_N| < 3e   , dove per gli esterni si è sfruttata la convergenza uniforme della l_n e per il termine centrale la 2ª ipotesi del teorema.

 

 

5) Se la successione di funzioni continue f_n converge uniformemente Þ il suo limite f è una funzione continua.

Si dimostra applicando il teorema dello scambio dei limiti alla funzione .

 

 

6) Teorema dello scambio del limite con la derivata :

Si abbia una successione di funzioni f_n : A®Â derivabili e

a)    la successione delle derivate {f_n^´} converge uniformemente in (a,b) con limite g

b)    la successione delle funzioni {f_n} converge almeno in un punto t₀ Î (a,b)

Þ           anche la successione f_n converge uniformemente in (a,b) e si ha

a) Si deve dimostrare che {f_n} converge uniformemente, ossia è rispettata la condizione necessaria e sufficiente di convergenza |f_n(t) - f_m(t)| < e a tal fine si applica il teorema di Lagrange  da cui sfruttando la convergenza puntuale in t₀ e l´uniforme convergenza della successione delle derivate {f_n^´} si  stabilisce l´uniforme convergenza ad f(t) della successione {f_n }.

b) Supponiamo che {f_n(t)} converga uniformemente ad f(t) mostro che f è derivabile, si ha :  da cui essendo il rapporto incrementale derivabile come si ottiene applicando ancora Lagrange e la convergenza uniforme della serie delle derivate, si possono scambiare i due limiti ottenendo  da cui la tesi.

 

 

7)    Teorema dello scambio del limite con l´integrale :

Si abbia una successione f_n di funzioni limitate integrabili sull´intervallo [a,b] , convergente uniformemente con limite f

Þ          

Si ha   in quanto la successione f_n converge uniformemente ad f .   Si deve solo dimostrare l´integrabilità di f  la quale si fa in termini di suddivisioni sfruttando l´uniforme convergenza di f_n ad f .

Serie di funzioni

8) Criterio di Convergenza puntuale di Cauchy :

Condizione necessaria e sufficiente perché la serie di funzioni Sx_n(t) converga puntualmente in A è che, fissato e > 0,

" tÎA esista N(e,t) tale che :            |x_p(t)+ x_p+1(t)+ ... + x_p+q(t)| < e                              se n, m > N            .

 

 

9) Criterio di Convergenza uniforme :

Condizione necessaria e sufficiente perché la serie di funzioni Sx_n(t) converga uniformemente in A è che, fissato e > 0, esista N(e) tale che :                |x_p(t)+ x_p+1(t)+ ... + x_p+q(t)| < e                " tÎA                  se n, m > N            .

 

 

10) Criterio di Weierstrass :

Data la successione di funzioni x_n  ed una serie convergente di costanti positive Sc_n   e definitivamente si ha |x_n(t)| £ c_n 

Þ  la serie di funzioni Sx_n(t) converge uniformemente in A.

Si dimostra in virtù della disuguaglianza triangolare e del criterio di convergenza di Cauchy dal quale deriva

|x_p(t)+ x_p+1(t)+ ... + x_p+q(t)| < |x_p(t)| + |x_p+1(t)| + ... + |x_p+q(t)| < c_p +  c_p+1 + ... + c_p+q < e

 

 

11) Teorema della convergenza totale :

Se {x_n} è una successione a valori in uno spazio di Banach (normato e completo) la cui serie delle norme S||x_n || è convergente                               Þ           converge anche la serie Sx_n  .

La dimostrazione ricalca quanto già ricavato per la convergenza assoluta delle serie numeriche, sfruttando analogamente il Criterio di convergenza puntuale di Cauchy e la disuguaglianza triangolare. Il teorema è detto della convergenza totale in quanto una serie per la quale converge la serie delle norme è detta totalmente convergente.

 

 

12) Teorema del limite di una serie :

Se Sf_n(t) è una serie di funzioni uniformemente convergente con somma F(t) ed esiste il limite  

Þ la serie Sl_n converge e si ha   

 

13) La somma di una serie uniformemente convergente di funzioni continue è una funzione continua.

Si deve dimostrare la continuità della somma della serie che ricordiamo essere pari alla somma del resto n-esimo e della somma parziale n-esima, considerando l´incremento h si hanno le due seguenti uguaglianze :

    e       sottraendo membro a membro si ottiene :

Dove per la 1ª quadra si sfrutta che S_n(x) è somma di funzioni continue e pertanto continua mentre per la 2ª e la 3ª quadra si sfrutta che la serie è uniformemente convergente quindi il resto n-esimo può essere reso piccolo quanto si vuole.

 

14) Teorema della integrale di una serie :

Si abbia una successione f_n di funzioni limitate integrabili sull´intervallo [a,b] , se la serie Sf_n(t) converge uniformemente in (a,b) con somma F(t)                         Þ           F è integrabile e si ha        

Si ricorda che la somma di una serie S è pari alla somma parziale n-esima S_n(x) più il resto n-esimo R_n(x) , integrando e passando ai moduli si ha :   

dove si è sfruttata la convergenza uniforme della serie. Pertanto il teorema è dimostrato.

 

 

15) Teorema della derivata di una serie :

Si abbia una successione f_n di funzioni derivabili e

a)    la serie delle derivate Sf_n^´ converge uniformemente in (a,b) con somma G(t)

b)    la serie delle funzioni   Sf_n converge almeno in un punto t₀ Î (a,b)

Þ   anche la serie Sf_n converge uniformemente in (a,b) e si ha

Sia g(x) =Sf_n´   essendo uniformemente convergente per il teorema precedente può essere integrata termine a termine

     dove nell´ultimo passaggio si è sfruttata la convergenza alla sua somma della serie di funzioni. Derivando la precedente espressione si ottiene g(x) = S´(x) e dunque in definitiva  S´(x) = Sf_n´   .

Serie di potenze

16) Se una serie di potenze converge uniformemente in un punto z₀ Î C

Þ           converge assolutamente in ogni punto tale che |z| < |z₀| 

Si ottiene per confronto con la serie geometrica infatti si ha 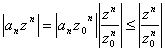   dove si è sfruttata la convergenza nel punto z₀ per maggiorare con 1 il termine  . L´ultima serie è geometrica e converge Û |z| < |z₀| nel qual caso il rapporto è minore di uno allora per il teorema del confronto anche è assolutamente convergente.

 

 

17) Criterio della radice per determinare il raggio di convergenza :

Data la serie sia    Þ           r = 1/l   è  il raggio di convergenza :

 

 

18) Criterio del rapporto per determinare il raggio di convergenza :

Data la serie se esiste il limite 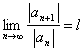          Þ           r = 1/l   è  il raggio di convergenza :

 

 

19) Proprietà della somma di una serie di potenze :

a)    La serie converge uniformemente in ogni cerchio :   |z| £ r´      con r´ < r

b)    La somma della serie è una funzione continua in  |z| < r

c)    La serie delle derivate è ancora una serie di potenze che ha lo stesso raggio di convergenza

d)    La somma della serie è derivabile in senso complesso con derivata continua in |z| < r ; la sua derivata è pari alla somma della serie delle derivate

a)   Si dimostra mediante il teorema di Weierstrass infatti la serie converge assolutamente per z = r´ essendo esso interno al raggio di convergenza e situato sulla asse reale pertanto abbiamo trovato una serie di costanti positive Sa_nr´ che converge e che maggiora la nostra serie Sa_nzⁿ  che pertanto converge assolutamente.

b)    Ricordando che la somma f(z) di una serie uniformemente convergente di funzioni continue è continua e data l´uniforme convergenza di Sa_nzⁿ appena dimostrata e la arbitrarietà del punto r´ , il teorema risulta dimostrato.

c)    Si ha che è una serie di potenze con coefficienti b_n  =(n+1)a_n+1 , applicando il criterio della radice si ottiene  e quindi il raggio di convergenza è lo stesso di a_n .

d)    E´ sufficiente scrivere f_x e f_y e verificare che soddisfano le relazioni di Cauchy - Riemann.

 

 

20) Altre proprietà della somma di una serie di potenze :

a)    La somma della serie di potenze è di classe C^¥ in    |z| < r

b)    La derivata k-esima della somma della serie è pari alla somma della serie delle derivate k-esime.

c)    Tra i coefficienti della serie e le derivate della somma f(z) sussiste la relazione

a)   Segue dal fatto che la serie delle derivate è ancora una serie di potenze con lo stesso raggio di convergenza.

b)    E´ esattamente il punto d) del teorema 19)

c)    Si ottiene in maniera pratica derivando la somma della serie

 

 

21) Teorema di Abel :

Se una serie di potenze Sa_nzⁿ  converge in uno dei punti estremi del suo intervallo di convergenza

Þ L´intervallo di convergenza include anche questo punto.

L´uniforme convergenza si ha se si dimostra che il resto n-esimo è minore di e 

essendo    si può scrivere   da cui raccogliendo xⁿ si ha  si può quindi sfruttare l´uniforme convergenza che rende tutti i resti n-esimi minori di e / 2   raccogliendo i quali rimane dentro parentesi lo sviluppo della serie geometrica per la quale la somma è  semplificando si ottiene che il resto n-esimo è minore di e .

22) Condizione necessaria per la sviluppabilità in serie di Taylor di una funzione f :

Sia f Î C^¥ (-r , r) ed esista una costante M, indipendente da n e da x tale che si abbia, definitivamente  Þ f è sviluppabile in serie di taylor in (-r , r).

Si sostituisce la condizione nel resto n-esimo  ottenendo 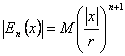 che tende a 0 per n che tende ad ¥.