Teoremi sul calcolo differenziale e l'approssimazione di funzioni
Calcolo differenziale
1) Se f è derivabile in x0 appartenente ad un intervallo Þ f è continua in x0 .
Per essere continua la funzione deve aversi che ![]() e dato che se f è derivabile in x0 allora deve essere finito il limite
e dato che se f è derivabile in x0 allora deve essere finito il limite ![]() ossia la f(x) è approssimabile in x0 da una retta tangente di equazione
ossia la f(x) è approssimabile in x0 da una retta tangente di equazione
y = f(x0) + f ´(x0)*(x-x0) detta di migliore approssimazione lineare in particolare f(x) e la retta distano tra di loro o(x-x0).
Si ottiene pertanto che![]() cioè f è continua in x0 .
cioè f è continua in x0 .
1-a) La derivata del prodotto di una funzione per una costante è pari alla costante moltiplicata per la derivata della f.
1-b) La derivata della somma (differenza) di 2 funzioni è pari alla somma (differenza) delle derivate delle 2 funzioni.
1-c) Derivata del prodotto di 2 funzioni derivabili :
Descrizione : ![]()
Nella definizione di derivata ![]() applicata alla funzione (fg)´ si somma e sottrae al numeratore f(x0)g(x) e si scinde quindi il rapporto nei 2 rapporti incrementali f ‘(x0) e g‘(x0) moltiplicati rispettivamente per g(x) e per f(x0). È solo la continuità in x0 che ci consente di sostituire g(x) con g(x0).
applicata alla funzione (fg)´ si somma e sottrae al numeratore f(x0)g(x) e si scinde quindi il rapporto nei 2 rapporti incrementali f ‘(x0) e g‘(x0) moltiplicati rispettivamente per g(x) e per f(x0). È solo la continuità in x0 che ci consente di sostituire g(x) con g(x0).
2) Derivata del rapporto di 2 funzioni derivabili :
Descrizione : 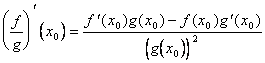
Si utilizza prima la definizione di derivata ![]() applicata alla funzione (1/g) e si ottiene
applicata alla funzione (1/g) e si ottiene 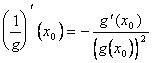 dopodiché si applica il 65-c) alla 1/g e ad f.
dopodiché si applica il 65-c) alla 1/g e ad f.
3) Formula di Leibnitz per il calcolo della derivata n-esima del prodotto di 2 funzioni derivabili:
Descrizione : ![]()
In pratica i coefficienti sono quelli del triangolo di Tartaglia ed il 1° indice della derivata scende mentre il 2° indice sale.
4) Se g è derivabile in x0 ed f è derivabile in g(x0) allora la funzione composta è derivabile in g(x0) :
Descrizione : ![]()
Si scrive la consueta versione estesa della derivata sia per g : ![]()
Che per f°g : ![]()
e sostituendo la 1ª nella 2ª il teorema risulta dimostrato.
5) Se una funzione f continua e strettamente monotona su di un intervallo (pertanto invertibile e l´inversa è continua nel suo dominio) e se questa è derivabile in x0 e diversa da 0 , Þ l´inversa è derivabile in f(x0).
Descrizione : ![]()
Si applica la definizione di derivata![]() nella quale si possono sostituire le corrispondenti x infatti f -1(y)®x , f -1(y0)®x0 , y0 ®f (x0) e y®f (x) ed il teorema risulta dimostrato.
nella quale si possono sostituire le corrispondenti x infatti f -1(y)®x , f -1(y0)®x0 , y0 ®f (x0) e y®f (x) ed il teorema risulta dimostrato.
6) (x a)´ = ax a -1
Si dimostra con la definizione coincisa di derivata ossia ![]() con h = x0 - x .
con h = x0 - x .
In particolare in essa occorre sostituire f(x+h) con (x+h)a ed f(x) con xa si fa in modo di raccogliere all´esterno x a -1 e poi sul restante internamente alla parentesi si utilizza il limite notevole (1+x)a = 1 + ax +o(x).
7) (ex)´ = ex
Si dimostra con la definizione coincisa di derivata ossia ![]() con h = x0 - x .
con h = x0 - x .
In particolare in essa occorre sostituire f(x+h) con e x+h ed f(x) con ex si raccogliere all´esterno ex e poi sul restante internamente alla parentesi si utilizza il limite notevole (ex - 1)/x ® 1 per x ®0 .
8) (sinhx)´ = coshx
Ricordando che sinhx = (ex - e -x)/2 derivarlo si riduce ad osservare che la costante può essere portata fuori mentre la derivata della differenza è pari alla differenza delle derivate, di cui la derivata di e-x si calcola come derivata di una funzione composta alla funzione non derivata per la derivata della argomento, sostituendo si trova la definizione di coshx.
9) (coshx)´ = sinhx
Ricordando che coshx = (ex + e -x)/2 si dimostra in maniera del tutto analoga a quanto fatto per sinhx.
10) (loga|x|)´ = (logae)/x
Si dimostra con la definizione coincisa di derivata ossia ![]() con h = x0 - x .
con h = x0 - x .
In particolare in essa occorre sostituire f(x+h) con loga|x+h| ed f(x) con loga|x| si raccogliere all´esterno 1/x in modo da riportarsi al logaritmo che moltiplica la definizione di e come limite di una successione
11) (ax)´ = ax log a
Ricordando che ![]() si applica a quest´ultima la regola di derivazione per le funzioni composte e sul risultato si considera log a giustamente come una costante.
si applica a quest´ultima la regola di derivazione per le funzioni composte e sul risultato si considera log a giustamente come una costante.
12-a) (sinx)´ = cosx
Si dimostra con la definizione coincisa di derivata ossia ![]() con h = x0 - x .
con h = x0 - x .
In particolare in essa occorre sostituire f(x+h) con sin(x+h) ed f(x) con sinx e poi si utilizza la formula per il seno di una somma ossia sen(a+b) = senacosb + cosasenb ed infine il limite notevole senx/x ®1 per x®0.
12*-b) (cosx)´ = - sinx
Si dimostra con la definizione coincisa di derivata ossia ![]() con h = x0 - x .
con h = x0 - x .
In particolare in essa occorre sostituire f(x+h) con cos(x+h) ed f(x) con cosx e poi si utilizza la formula per il coseno di una somma ossia cos(a+b) = cosacosb - senasenb.
13) (tgx)´ = 1+tg2x = 1/ cos2x
Si dimostra ricordando che tgx = senx / cosx ed utilizzando la regola per la derivata del rapporto di 2 funzioni derivabili.
14-a) (arcsinx)´ = ![]()
Occorre applicare il teorema per la derivazione della funzione inversa. A tal uopo osserviamo che
a) arcsinx è l´inversa di senx la quale è una funzione strettamente crescente in [-p/2 , p/2] ed avente come derivata la funzione cosx che nell´intervallo (-p/2 ,p/2) è sempre ¹ 0 pertanto non avremo mai che l´inversa ha una tangente verticale e quindi è sempre derivabile.
14-b) si pone y = arcsinx e utilizzando il teorema si ha ![]() quindi
quindi 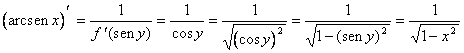
dove nell´ultimo passaggio si è sfruttato che se y = arcsinx allora è anche vero che x = seny.
15-a) (arccosx)´ = ![]()
Si dimostra in maniera analoga a quanto fatto per arcsinx.
16) (arctgx)´ = ![]()
Occorre applicare il teorema per la derivazione della funzione inversa. A tal uopo osserviamo che
a) arctgx è l´inversa di tgx la quale è una funzione strettamente crescente in [-p/2 , p/2] ed avente come derivata la funzione 1+tg2x ³ 1 nell´intervallo (-p/2 ,p/2) è pertanto sempre ¹ 0 quindi non avremo mai che l´inversa ha una tangente verticale e quindi è sempre derivabile.
b) si pone y = arctgx ed utilizzando il teorema ![]() si ottiene :
si ottiene : ![]()
dove nell´ultimo passaggio si è sfruttato che se y = arctgx allora è anche vero che x = tgy.
17) (|x|)´ = sgnx
Si dimostra con la definizione coincisa di derivata ossia ![]() con h = x0 - x .
con h = x0 - x .
In particolare in essa occorre sostituire f(x+h) con |x+h| ed f(x) con |x| dopochè visto che h®0 la si suppone trascurabile e sciogliendo i moduli si ottiene a 2 diverse frazioni, quella per x >1 ha come limite 1 mentre quella per x < 1 ha come limite -1 il che coincide con la definizione della funzione sgnx.
18) Se f è derivabile in x0 Î (a,b) ed f ha un estremo locale in x0 Þ f ´(x0) = 0
Dimostriamo il caso in cui x0 è un punto di massimo locale.
Dovrà esistere un intorno di x0 nel quale la f(x) < f(x0) ossia f(x) - f(x0) < 0 per x compresa tra (x0 - e) ed (x0 + e).
Il rapporto incrementale ![]() avrà dunque il numeratore minore di 0 pertanto :
avrà dunque il numeratore minore di 0 pertanto :
* se ci troviamo a sinistra di x0 il denominatore è negativo pertanto ![]() e così pure il limite ossia la derivata sinistra in x0.
e così pure il limite ossia la derivata sinistra in x0.
* se ci troviamo a destra di x0 il denominatore è positivo pertanto ![]() e così pure il limite ossia la derivata destra in x0.
e così pure il limite ossia la derivata destra in x0.
Per la derivabilità di f in x0 deve essere il limite da destra uguale al limite da sinistra, condizione che è solo rispettata se f´(x0) = 0.
19) Teorema di Rolle:
Descrizione : Se f è continua in [a,b] e derivabile in (a,b) e se f(a) = f(b) Þ esiste un punto c tale che f ‘(c) = 0.
Essendo f una funzione continua su di un compatto allora ammette Min e Max e pertanto si possono verificare :
a) se la funzione è costante f(a) = f(b) = f(c) = Min = Max pertanto f ‘(c) = 0 per ogni c Î (a,b) .
b) Se Max > f(a) allora deve esistere almeno un punto di estremo c nel quale la 81) ci dice che f ‘(c) = 0, analogamente se Min < f(a).
20) Teorema di Cauchy:
Descrizione : Se f e g sono funzioni continue in [a,b] e derivabili in (a,b) Þ esiste un punto c Î (a,b) tale che
(f(b)-f(a))g‘(c) = (g(b)-g(a))f ‘(c).
Mi riconduco a poter applicare il teorema di Rolle definendo su [a,b] una funzione h := (f(b) - f(a))g(x) - (g(b) - g(a))f (x) tale che h(a) = h(b) dovrà pertanto esistere un punto di estrem c nel quale h´(c) = 0. Imponendo che la derivata 1ª di h(x) (si considerino (f(b) - f(a)) e (g(b) - g(a)) come costanti ) sia uguale a 0 ottengo la formula di Cauchy.
21) Teorema del valor medio:
Descrizione : Se f è continua in [a,b] e derivabile in (a,b) Þ esiste un punto c tale che ![]()
Si dimostra ponendo g(x) = x nel teorema di Cauchy.
22) Se f è continua in [a,b], derivabile in (a,b) e se esiste ![]() Þ
Þ ![]()
Per il teorema del valor medio esiste un punto c tale che ![]() , facendo il limite per c ® a+ si ottiene il risultato.
, facendo il limite per c ® a+ si ottiene il risultato.
23) Se f è derivabile in (a,b) Þ f ´ non ammette discontinuità di 1ª specie (di salto)
Il teorema 22) ci dice che se dovessero esistere i 2 limiti da destra e da sinistra nel punto x0 allora questi sarebbero uguali a f ´+(x0) e a f ´-(x0) ma la derivabilità implica che f ´+(x0) = f ´-(x0) pertanto non ci possono essere discontinuità di salto, sono invece possibili discontinuità di 2ª specie.
24) Se F e G sono funzioni primitive in un intervallo I della stessa f Þ esiste una costante C Î Â tale che
G(x) = F(x) + C " xÎI
Viene definita una funzione g(x) pari alla differenza tra G(x) ed F(x) , la sua derivata prima è la differenza delle derivate prime di G(x) e di F(x) le quali però coincidono con f di cui F e G sono primitive per ipotesi del teorema, quindi g´(x)= 0.
Applicando il teorema del valor medio si ottiene ![]() e pertanto g(x2) = g(x1) e per la arbitrarietà di x1 ed x2 segue che g è costante quindi le 2 primitive F e G sono uguali a meno di una costante.
e pertanto g(x2) = g(x1) e per la arbitrarietà di x1 ed x2 segue che g è costante quindi le 2 primitive F e G sono uguali a meno di una costante.
25) Se una funzione f definita su di un intervallo ha una discontinuità di 1ª specie Þ f non ammette primitive.
Se per assurdo dovesse esistere una primitiva, la sua derivata, ossia f avrebbe una discontinuità di 1ª specie il che è impossibile come dimostrato al punto 86) dove si affermava che se una funzione f è derivabile allora la sua derivata 1ª non può ammettere discontinuità di 1ª specie o di salto.
26) Se f è derivabile in un intervallo ed f ‘ è in esso limitata ossia esiste un L tale che | f ´(x) | £ L Þ f è lipschitziana nell´intervallo con costante di Lipschitz L ossia ![]() .
.
Posso scegliere arbitrariamente x ed y e trovare per il teorema del valor medio un punto ad essi interno che ha la stessa derivata della retta che congiunge x ed y e siccome questa derivata deve essere £ L segue che questo sarà vero " x, y .
e dunque la funzione è lipschitziana.
27) Se una funzione è derivabile in (a,b) Þ
a) f ‘(x) ³ 0 " xÎ(a,b) Û f è crescente in (a,b)
b) f ‘(x) £ 0 " xÎ(a,b) Û f è decrescente in (a,b)
c) f ‘(x) > 0 " xÎ(a,b) Þ f è strettamente crescente in (a,b)
d) f ‘(x) < 0 " xÎ(a,b) Þ f è strettamente decrescente in (a,b)
Dimostro solo il caso a) in quanto le altre dimostrazioni sono analoghe.
Þ Ipotizzando che sia a < x1 < x2 < b , applicando il teorema del valor medio, esisterà un punto c nel quale
f(x2) - f(x1) = f ‘(c)(x2 - x1) ³ 0 in quanto f ‘(x) ³ 0 per ipotesi del teorema mentre (x2 - x1) ³ 0 in quanto x1 precede x2 per nostra ipotesi quindi f(x2) ³ f(x1) " x1 , x2 da cui segue che la funzione è crescente.
Ü Se f è crescente allora il rapporto incrementale non può che essere ³ 0 e così pure la derivata 1ª che ne è il limite per x ® x0 .
28) Teorema di de L´Hopital :
Descrizione : Se f e g sono 2 funzioni derivabili in (a,b) e soddisfano le 3 seguenti ipotesi :
a) ![]()
b) g´(x) ¹ 0 per ogni xÎ(a,b)
c) ![]()
allora si ha che anche ![]() .
.
dalla c) deriva che vi deve essere un intorno ![]() , del resto questa equivale alla
, del resto questa equivale alla ![]() per il teorema di Cauchy infatti se f e g sono funzioni continue in [a,b] e derivabili in (a,b) allora, presi 2 punti x,y in un intorno destro di a, esiste un punto c Î (a,b) tale che
per il teorema di Cauchy infatti se f e g sono funzioni continue in [a,b] e derivabili in (a,b) allora, presi 2 punti x,y in un intorno destro di a, esiste un punto c Î (a,b) tale che ![]() . Al tendere y®a+ , per la ipotesi a) si ha che
. Al tendere y®a+ , per la ipotesi a) si ha che ![]() ossia
ossia ![]() il che dimostra il teorema.
il che dimostra il teorema.
Approssimazione polinomiale
29-a) Formula di Taylor:
Descrizione : ![]()
Al fine di effettuare una approssimazione della f(x) per x®x0 si estrapolano le seguenti osservazioni :
a) Se f(x) è continua Þ f(x) = f(x0) + o(1) = T0(x0)
b) Se f(x) è derivabile Þ f(x) = f(x0) + f ´(x0)(x - x0) + o(x - x0) = T1(x0)
In generale quindi la approssimazione si realizza imponendo il contatto di ordine n tra la funzione ed il polinomio, in particolare si dovrà avere Tn(K)(x0) = f (K) (x0). Intuitivamente si deduce che il polinomio di Taylor di ordine n debba assumere la forma Tn(x) = a0 + a1(x-x0) + a2(x-x0)2 + ... + an(x-x0)n nella quale il valore del termine ax può essere ricavato imponendo che Tn (K)(x0) = f (K) (x0) Û k !an = f (K) (x0) e quindi an = (f (K) (x0) )/ (k !) e si potrà in definitiva quindi scrivere il polinomio ![]()
29-b) Formula di Mac Laurin
Descrizione : ![]() non è altro che la formula di Taylor con x0 = 0.
non è altro che la formula di Taylor con x0 = 0.
30) Teorema di Peano
Descrizione : Se f è n volte derivabile in x0 il polinomio di Taylor di grado n ![]() è l´unico polinomio di grado £ n tale che :
è l´unico polinomio di grado £ n tale che :
a) f(x) = Tn(x) + o((x-x0)n) per x®x0
b) Tn(K)(x0) = f (K)(x0)
b) deriva dalle considerazioni svolte nella costruzione del polinomio.
a) Che Tn(x) sia un polinomio con queste caratteristiche si ricava per induzione infatti :
* E´ vero per T0(x) = f(x0) + o(1)
* E´ vero per T1(x) = f(x0) + f ‘(x0)(x-x0) + o(x-x0)
** Supponiamo che sia vera per ogni funzione derivabile n-1 volte e si ha f(x) = Tn - 1(x) + o((x-x0) n - 1)
pertanto applicando de l´Hopital si ha che 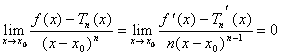
Dove nell´ultimo passaggio si sfrutta ** osservando che ![]() è il polinomio di Taylor di grado n -1 di
è il polinomio di Taylor di grado n -1 di ![]() .
.
L´unicità del polinomio di Taylor si dimostra considerando un P(x+dx) di grado £ n tale che f(x) = P(x) + o((x-x0) n ) per x®x0 , del resto è anche f(x) = Tm(x) + o((x-x0)n) , uguagliando si ha : P(x) - Tn (x) = o((x-x0) n ) e dato che entrambe i polinomi sono di grado £ n ne consegue che o((x-x0) n ) non è in grado di assorbire nessun termine degli stessi e dunque P(x) = Tn(x).
31) Se f è derivabile in x0Î(a,b) almeno n ³ 2 volte e se tutte le derivate di ordine inferiore ad n sono nulle in x0 allora
n è pari Û x0 è un punto di minimo locale forte se la derivata ennesima di f in x0 è > 0
x0 è un punto di massimo locale forte se la derivata ennesima di f in x0 è < 0
n è dispari Þ x0 non è un punto di estremo
Dal teorema di Peano, considerando che tutte le derivate di ordine minore di n sono nulle in x0 segue che
![]() per x ® x0
per x ® x0
se n è pari (x-x0) ³ 0 e pertanto se f (n)(x0) > 0 allora c´è un minimo in x0 in quanto in un suo intorno f(x) > f(x0)
mentre se f (n)(x0) < 0 allora c´è un massimo in x0 in quanto in un suo intorno f(x0) > f(x)
se n è dispari il segno della f(x)-f(x0) dipende sia dal segno della derivata che dalla posizione in cui si trova l´x considerato rispetto ad x0 , in particolare si potrà notare che se ad esempio a sinistra f(x) > f(x0) ebbene a destra si ha il contrario quindi x0 non è un estremo locale.
Funzioni convesse
32) Una funzione è strettamente convessa in (a,b) Û " a < x1 < x2 < x3 < b si ha la seguente relazione d´ordine :
P(x1,x2) £ P(x1,x3) £ P(x2,x3) essendo P la pendenza della congiungente i 2 punti.
33) Se ho una funzione convessa Þ
a) " xÎ(a,b) esistono finiti il limite delle derivate prime da destra e da sinistra
b) " xÎ(a,b) il limite della derivata prima da destra è maggiore del limite della derivata prima da sinistra
c) La derivata prima da destra e la derivata prima da sinistra sono crescenti in (a,b)
d) f è una funzione continua in (a,b)
a) L´esistenza del limite finito per le derivate destre e sinistre in ogni punto appartenente ad (a,b) si dimostra semplicemente prendendo 5 punti di cui quello centrale è x0 , il 2° è x che tende ad x0 da sinistra ed il 4° è y che tende ad x0 da destra ebbene facendo tendere x a x0 ,il limite della pendenza della congiungente corrisponde alla derivata prima da sinistra in x0 ed è limitata superiormente (per il 95) dalla pendenza della retta che unisce x0 con il 5° punto, pertanto questo limite esiste finito in quanto per una funzione monotona il limite esiste sempre, esso è +¥ se la funzione non è limitata mentre se la funzione è limitata, esisto finito il limite. Analogamente facendo tendere y a x0 il limite della pendenza della congiungente corrisponde alla derivata prima da destra in x0 ed è limitata inferiormente (per il 95) dalla pendenza della retta che unisce x0 con il 1° punto.
b) La derivata da destra in x0 è maggiore della derivata da sinistra in quanto ogni punto a destra di x0 ha pendenza inferiore rispetto ad ogni punto a sinistra di x0 effettuando il limite delle pendenze il teorema è dimostrato.
c) Si dimostra che f ´+ è crescente ricordando che f ´+ non è altro che il limite per h®0 di P(x , x+h), quindi considerando x1 < x2 si deve dimostrare che f ´+(x1) < f ´+(x2) ossia P(x1 , x1+h) < P(x2 , x2+h) il che avviene in base al 95) e disegnando una funzione convessa e sulle ascisse i punti a , x1 , x1 + h, x2 , x2 + h, b si hanno le due disuguaglianze P(x1 , x1+h) < P(x1 , x2+h) e P(x1 , x1+h) < P(x1 , x2+h) quindi si ha anche P(x1 , x1+h) < P(x2 , x2+h). Al tendere h®0 il teorema è dimostrato.
d) L´esistenza del limite per la derivata prima sia da destra che da sinistra implica la continuità sia da destra che da sinistra infatti se una funzione è derivabile in un punto è anche continua in quel punto.
34) f è convessa in (a,b) Û esistono finite le derivate da destra e da sinistra in ogni punto e sono funzioni crescenti.
35-a) Se f è derivabile in (a,b) le seguenti affermazioni sono equivalenti:
a) f è (strettamente) convessa in (a,b)
b) f ‘ è strettamente crescente in (a,b)
c) " x0Î(a,b) la funzione si trova al di sopra della retta tangente di migliore approssimazione lineare in x0
a) e b) se ne dimostra l´equivalenza direttamente osservando che derivabile significa f ‘+ = f ‘- = f ‘ e poi applicando il 97).
c) se ne dimostra l´equivalenza ad a) ricordando che nel 96) avevamo stabilito che la pendenza rispetto ad x0 è maggiore per i punti a destra di x0 che non per i punti a sinistra di x0 il che può essere riassunto nella formula f(x) - f(x0) ³ f ‘(x0)(x-x0) che si può anche scrivere f(x) ³ f(x0) + f ‘(x0)(x-x0) dove il 2° membro è la retta di migliore approssimazione lineare in x0 .
35-b) Se f è 2 volte derivabile in (a,b) allora
a) f è convessa in (a,b) Û f ´´ ³ 0 in (a,b)
b) f ´´ > 0 Þ f è strettamente convessa in (a,b)
La f convessa abbiamo visto nel 98-a) implica che la derivata prima è strettamente crescente pertanto essendo la derivata seconda corrispondente alla derivata prima di f ‘ essa è ³ 0 in quanto derivata di una funzione crescente.
36) Se f ha un flesso in x0 Î (a,b) ed è 2 volte derivabile in x0 Þ f ‘´(x0) = 0
Viene definita una funzione u(x) := f(x) - f(x0) - f ‘(x0)(x - x0) , per essa si ha u´(x0) = 0 Þ u´(x) = f ‘(x) ed f ´(x) = 0 in quanto dal lato di x0 dove f è convessa si ha u(x) ³ 0 mentre dalla altro lato dove f è concava si ha u(x) £ 0. Del resto per il 94) anche u´´(x0) = 0 in quanto u(x) non ha un estremo locale in x0 ed n è pari, del resto u´´(x0) = f ´´(x0) quindi f ‘´(x0) = 0.
Errore nella approssimazione con il polinomio di Taylor
37) Se f è una funzione n volte derivabile in [a,b] , n+1 volte derivabile in [a,b]/{0} e la derivata n-esima è continua in [a,b] Þ per ogni xÎ[a,b] x¹x0 , esiste un q Î(0,1) : 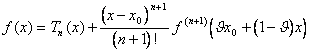
Per dimostrare il teorema vengono definite 2 funzioni,
u(x) := f(x) - Tn(x) le cui derivate in x0 sino all´ordine n sono 0 mentre la derivata in x di ordine n+1 è un+1(x) = f (n+1)(x)
v(x) := (x-x0)n+1 le cui derivate in x0 sino all´ordine n sono 0 mentre la derivata in x di ordine n+1 è vn+1(x) = (n+1)!
Dovendo giungere al risultato che 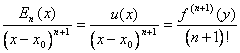 applichiamo ricorsivamente il teorema di Cauchy sino a giungere alla derivata di ordine n+1 sfruttando in ogni passaggio che le derivate sino al grado n sono nulle in x0 , in particolare, applicando una 1ª volta il teorema di Cauchy si identifica un punto y1 nel quale il rapporto tra le due funzioni è pari al rapporto tra le 2 derivate prime. Applicando una 2ª volta questo teorema all´intervallo (x0 , y1) si determina un punto y2 nel quale il rapporto delle derivate seconde è pari al rapporto delle funzioni. Procedendo ulteriormente, al passo n+1 si individua un punto y n +1 nel quale è verificato quanto esposto dal teorema ossia
applichiamo ricorsivamente il teorema di Cauchy sino a giungere alla derivata di ordine n+1 sfruttando in ogni passaggio che le derivate sino al grado n sono nulle in x0 , in particolare, applicando una 1ª volta il teorema di Cauchy si identifica un punto y1 nel quale il rapporto tra le due funzioni è pari al rapporto tra le 2 derivate prime. Applicando una 2ª volta questo teorema all´intervallo (x0 , y1) si determina un punto y2 nel quale il rapporto delle derivate seconde è pari al rapporto delle funzioni. Procedendo ulteriormente, al passo n+1 si individua un punto y n +1 nel quale è verificato quanto esposto dal teorema ossia 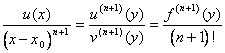 .
.