Concetti di base, funzioni, spazio reale, limiti
Dato un insieme ordinato X ed un suo sottoinsieme naturalmente ordinato A, allora un maggiorante di A è qualsiasi elemento di X che sia confrontabile con " elemento a di A e lo segua o sia ad esso uguale.
2) Insieme limitato superiormente:È un insieme avente almeno un maggiorante.
3) Estremo superiore:Dato un insieme ordinato X ed un suo sottoinsieme naturalmente ordinato A, allora un maggiorante di A è qualsiasi elemento di X che sia confrontabile con " elemento a di A e lo segua o sia ad esso uguale. Il più piccolo di questi maggioranti si chiama estremo superiore di A o Sup A. Tale estremo superiore è unico.
4) Massimo:Se il maggiorante della insieme A compreso in X oltre ad appartenere ad X appartiene anche ad A allora tale elemento si definisce Massimo e si indica con Max A. Tale massimo è unico.
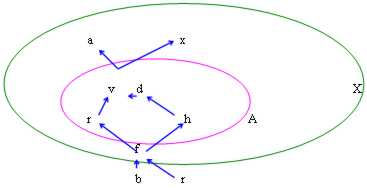
In questa figura abbiamo i seguenti casi:
maggioranti : v, a, x esistono quindi A è limitato superiormente
minoranti : f, b, x esistono quindi A è limitato inferiormente
Sup A : il più piccolo dei maggioranti è v
Inf A : il più grande dei minoranti è f
Max A : è sempre v in quanto oltre ad essere il più piccolo dei maggioranti è anche compreso in A
Min A : è sempre f in quanto oltre ad essere il più grande dei minoranti è anche compreso in A
5) Minorante:Dato un insieme ordinato X ed un suo sottoinsieme naturalmente ordinato A, allora un minorante di A è qualsiasi elemento di X che sia confrontabile con " elemento a di A e lo precede.
6) Insieme limitato inferiormente:È un insieme avente almeno un minorante.
7) Estremo inferiore:Dato un insieme ordinato X ed un suo sottoinsieme naturalmente ordinato A, allora un minorante di A è qualsiasi elemento di X che sia confrontabile con " elemento a di A e lo preceda . Il più grande di questi minoranti si chiama estremo inferiore di A o Inf A. Tale estremo inferiore è unico.
8) Minimo:Se il minorante della insieme A compreso in X oltre ad appartenere ad X appartiene anche ad A allora tale elemento si definisce Minimo e si indica con min A. Tale minimo è unico.
9) Insieme finito:Un insieme A si dice finito se ha un n° finito di elementi ossia esiste un n Î À tale che il n° di elementi di A è n.
Se un insieme ordinato A è finito e non vuoto allora esso ammette minimo e massimo.
10) Insiemi numerici:Sono insiemi costituiti da elementi chiamati “numeri” appartenenti all´insieme X x X ® X ossia ad una coppia di numeri in X è associato un solo n° in X che è funzione della operazione indicata.
Le operazioni sempre possibili in un insieme numerico sono le seguenti:
Addizione tra numeri con le seguenti 4 proprietà o assiomi:
a) ASSOCIATIVA Þ " x, y, z x + y + z = (x + y) + z = x + (y + z)
b) COMMUTATIVA Þ " x , y x + y = y + x
c) ZERO Þ " x Î x + 0 = x
d) NUMERO OPPOSTO Þ " x $ -x : x - x = 0
Moltiplicazione tra numeri con le seguenti 4 proprietà o assiomi:
a) ASSOCIATIVA Þ " x, y, z x (yz) = (xy)z = (xz)y
b) UNITA´ Þ " x x * 1 = x
c) COMMUTATIVA Þ " x, y xy = yx
d) RECIPROCO Þ " x ¹ 0 $! n° : x * x-1 = 1
Inoltre somma e moltiplicazione sono legate dalla seguente proprietà distributiva:
a) DISTRIBUTIVA SOMMA Þ " x, y, z x (y + z) = (xy) + (xz)
Sono inoltre definite le seguenti :
Proprietà di densità o della aggiungi un posto a tavola
Dati 2 elementi qualsiasi x e y, tra di essi esistono infiniti elementi di Q, che si possono ricavare facendo la media aritmetica tra x ed y, operazione che in Q è consentita.
Proprietà di Archimede o del salto
Dati 2 elementi qualsiasi x e y, di Q, con x < y allora esiste sempre un n° n che, moltiplicato per x, mi dà la relazione
nx > y
infatti basta considerare i ni come frazioni e porre n pari al prodotto tra il denominatore di x ed il numeratore di y.
11) Rappresentazione decimale:
È una rappresentazione che vede i numeri razionali espressi non come frazioni ma come insiemi di ni che si susseguono e rappresentanti essi stessi una frazione ma pesata. Si pensi a p , esso vale in notazione decimale
3.141592654 = ![]() i numeri decimali in questo caso sono illimitati e danno vita ad un n° reale a differenza delle frazioni tra ni primi che danno vita ad allineamenti decimali limitati o periodici con periodo ¹ 9 in quanto se il periodo è 9 si cade in un controsenso sviluppando le formule della successione..
i numeri decimali in questo caso sono illimitati e danno vita ad un n° reale a differenza delle frazioni tra ni primi che danno vita ad allineamenti decimali limitati o periodici con periodo ¹ 9 in quanto se il periodo è 9 si cade in un controsenso sviluppando le formule della successione..
Si definisce PROPRIO un allineamento decimale che non ha 9 come periodo.
In Q gli allineamenti decimali rispondono alla seguente:
se x > 0 come ad esempio p :
3.141592654 < = x < 3.141592654 + ![]()
cioè x è compreso tra il suo valore ed il suo valore più una anticchia, espressa da ![]()
se x < 0 come ad esempio - p :
- 3.141592654 - ![]() < x < = -3.141592654
< x < = -3.141592654
cioè x è compreso tra il suo valore meno una anticchia, espressa da ![]() ed il valore ricercato, ciò per via della incompletezza della insieme numerico Q.
ed il valore ricercato, ciò per via della incompletezza della insieme numerico Q.
12) Proprietà di completezza di Â:
Se un insieme A Î Â ,e pertanto ordinato, è limitato superiormente(inferiormente) ossia ammette almeno un maggiorante(minorante), allora esso ammette anche estremo superiore(inferiore) ossia esiste un maggiorante(minorante) che precede(segue) gli altri
Questo in altre parole ci dice che, un numero reale non è altro che una sezione tra due insiemi e rappresenta la estremo superiore del minore e la estremo inferiore del maggiore dei 2 insiemi.
Dim Þ si presentano due casi:
1) A è finito , esiste il massimo (è anche estremo superiore) di A essendo A totalmente ordinato.
2) A è infinito ed allora dobbiamo dimostrare che di tutti i maggioranti di A ce n´è uno che è più piccolo degli altri,
Procediamo per passi successivi ossia ;
* prendiamo un maggiorante y0 di A ed un elemento a0 di A.
* individuiamo il punto intermedio tra i due elementi che quindi divide l´intervallo in 2 altri intervalli.
* scegliamo l´intervallo contenente punti di A e se li hanno entrambi, scegliamo quello di sinistra.
* individuiamo il punto intermedio tra i due elementi che quindi divide l´intervallo in 2.
* continuiamo così finche l´intervallo tra un elemento di A ed i suoi maggioranti non diviene piccolissimo, tanto da ridursi ad un solo elemento che chiameremo y+ , o Sup A, questo si ricava dal fatto che la serie è non
decrescente ha limite superiore in ae e tende a y+ .
La lunghezza della ultimo intervallo vale (y0 - a0)/ 2n.
Gli intervalli così ottenuti sono come bambole russe contenute una nella altra.
yn > = a , " a Î A e " n ossia il valore della ultimo maggiorante trovato è ancora superiore ad a
dobbiamo ora dimostrare che questo numero sia realmente il Sup A ossia che risponda alle 2 seguenti:
a) " a Î A , a < = y+
Questo si dimostra per assurdo dicendo che esiste un elemento a+ di A che sia maggiore di y+ allora se prendiamo la distanza a+- y+ e la chiamiamo da+- y+ possiamo prendere un n tale da individuare un intervallo (y0 - a0)/ 2n ++ < da+- y+ ricaveremo che:
![]()
con n++ = n tale da individuare un maggiorante più piccolo di y+
y+ = SupA individuato dalle ripartizioni
yn++ = Y associato ad n++
questa formula ci porta ad un controsenso in quanto yn++ è minore di y+ che quindi è il vero Sup A.
b) " e < 0 $ a Î A : a > y+ - e
Ossia appena ci allontaniamo un pò da y+ la prima cosa che incontriamo è un elemento a di A.
Anche questo si dimostra per assurdo ponendo che " elemento a Î A , esso sia minore di y+ - e.
questo significherebbe che tra y+ - e , e yn non ci sono elementi di A ma se scegliamo un n++ che sia più piccolo di e allora nell´intervallo che esso delimita non ci sarà alcun punto di A, e questo è discorde con quello che era stato il nostro criterio di ricerca, pertanto è un assurdo.
Quanto dimostrato per la estremo superiore vale anche per la estremo inferiore.
N.B. La precedente dimostrazione è tratta da Analisi Matematica 1 ed è apparentemente diversa da quella che troviamo sulle Lezioni di A.m.1 in quanto quella ha un approccio legato ai numeri decimali illimitati.
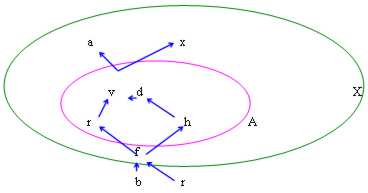
In  , v ed f esistono sempre se considerati come Sup A ed Inf A, non come Max A o Min A.
13) Teorema di Bolzano - Weierstrass :Abbiamo un insieme E Ì Ân con le seguenti caratteristiche:
* limitato (esiste un r > 0 tale che E è contenuto nell´intorno di centro O e raggio r)
* infinito (un insieme A si dice infinito se ha un n° infinito di elementi ossia non esiste un n Î À tale che il n° di elementi di A è n).
Allora in Ân esiste almeno un punto di accumulazione (punto nel cui intorno ci sono infiniti punti di E) di E.
Dimostrazione:
1) Dobbiamo trovare un candidato ad essere punto di accumulazione
così come abbiamo fatto per dimostrare la completezza di  analogamente ci muoviamo per Â2 , stavolta però invece di considerare intervalli su di una retta considereremo aree ed in particolare aree di rettangoli. Abbiamo supposto A limitato appositamente al fine di poterlo racchiudere in un cerchio ma sappiamo bene che racchiudendolo in un rettangolo non cambia nulla di determinante.
Chiameremo T0 questo rettangolo contenente il nostro insieme infinito E.
* suddividiamo T0 con proiezioni a , b , c , d in 4 parti uguali creando quindi altri 4 rettangoli
* Chiamiamo T1 il rettangolo che secondo noi contiene ¥ punti di E (ce n´è sicuramente 1 visto che E è un insieme infinito).
* Suddividiamo T1 in maniera analoga e riproduciamo la algoritmo sino ad individuare un rettangolo sufficientemente piccolo e che contenga ancora infiniti punti di E .
* abbiamo così le seguenti relazioni:
1) Il lato sx di un qualsiasi rettangolo così costruito non può che avere ascissa > o = al lato sx del rettangolo che lo precede e < o = al lato sx del rettangolo del quale è origine.
2) Il lato dx di un qualsiasi rettangolo così costruito non può che avere ascissa < o = al lato dx del rettangolo che lo precede e > o = al lato dx del rettangolo del quale è origine.
1°2) Qualsiasi rettangolo ottenuto nella serie avrà la ascissa del lato sx < della ascissa del lato dx di un qualsiasi altro rettangolo della serie.
3) Il lato basso di un qualsiasi rettangolo così costruito non può che avere ordinata > o = al lato basso del rettangolo che lo precede e < o = al lato basso del rettangolo del quale è origine.
4) Il lato alto di un qualsiasi rettangolo così costruito non può che avere ordinata < o = al lato dx del rettangolo che lo precede e > o = al lato alto del rettangolo del quale è origine.
3°4) Qualsiasi rettangolo ottenuto nella serie avrà l´ordinata del lato basso < della ordinata del lato alto di un qualsiasi altro rettangolo della serie.
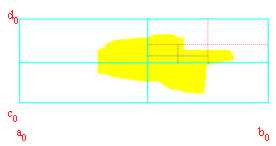
E quindi definendo:
A = insieme delle ascisse dei lati Dx della serie dei rettangoli.
B = insieme delle ascisse dei lati Sx della serie dei rettangoli.
C = insieme delle ordinate dei lati bassi della serie dei rettangoli.
D = insieme delle ordinate dei lati bassi della serie dei rettangoli.
* possiamo dire che qualsiasi elemento di B è maggiorante di un qualsiasi elemento di A
* possiamo dire che qualsiasi elemento di A è minorante di un qualsiasi elemento di B
pertanto per la proprietà di completezza, esiste il Sup A ed il Min B e nella fattispecie possiamo anche affermare che il Sup A < = Inf B e per rendere uguali i 2 valori dobbiamo far si che la distanza divenga 0 il che si ottiene lavorando sul lato basso della ultimo rettangolino che vale ![]() quantità che tende a zero al crescere di n, ossia del n° di rettangolini utilizzati. Pertanto possiamo scegliere n tale da ottenere Sup A = Inf B.
quantità che tende a zero al crescere di n, ossia del n° di rettangolini utilizzati. Pertanto possiamo scegliere n tale da ottenere Sup A = Inf B.
Analogamente ci comportiamo sugli insiemi C e D sino a determinare il Sup di C = Inf D.
Pertanto il nostro candidato è il punto x( Sup A, Inf D).
2) Dobbiamo ora dimostrare che questo punto è realmente un punto di accumulazione.
Deve essere cioè dimostrato che in un intorno di centro x e raggio e vi siano infiniti punti di E, ma questo avverrà sicuramente se di quei rettangolini che abbiamo utilizzato ve ne è uno che sia contenuto completamente nell´intorno del nostro punto di accumulazione, questo perchè ognuno di quei rettangolini era stato costruito col criterio che contenesse infiniti punti di E.
Ma per essere sicuri che il rettangolino cada nell´intorno dobbiamo far sì che la sua diagonale (diam Tn ) sia inferiore al raggio della intorno 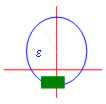
se la diagonale di T0 , diam T0 = ![]() allora diam Tn =
allora diam Tn = 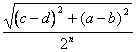
dobbiamo cioè porre ![]() ma questo è un n° che sicuramente esiste infatti il Teorema di archimede ci dice che basta moltiplicare r per un n° opportuno.
ma questo è un n° che sicuramente esiste infatti il Teorema di archimede ci dice che basta moltiplicare r per un n° opportuno.
In particolare si può inscrivere un quadrato nel cerchio e dimostrare che il rettangolino vi è contenuto pertanto il quadrato possiede infiniti punti di E e così anche l´intorno del nostro punto x che può quindi definirsi a pieno titolo come punto di accumulazione di un insieme E limitato ed infinito.
14) Topologia in ÂnSi definisce Topologia quella branca della matematica che si occupa dello studio di un´entità piccolissima, imprecisa, ma di grande utilità, l´intorno.
15) Intorno sferico:
Sia x Î Ân ed r Î Â,
si definisce come facente parte della intorno sferico di centro x e raggio r ogni punto la cui distanza da x sia inferiore ad Â. si distinguono i seguenti casi:
n = 1 Þ l´intorno delimita l´intervallo (x-r , x+r)con gli estremi esclusi.
n = 2 Þ L´intorno delimita dei cerchi concentrici di raggio inferiore ad r
n = 3 Þ L´intorno delimita delle sfere piene centrate in x e di raggio r prive del bordo.
16) Sfera:
Si definisce invece sfera di centro x Î Ân e raggio r Î Â, tutti i punti la cui distanza da x è esattamente r.
n = 1 Þ La sfera individua i soli 2 punti (x-r , x+r).
n = 2 Þ La sfera individua la sola circonferenza esterna, sono esclusi tutti i punti interni.
n = 3 Þ La sfera delimita unicamente il bordo delle sfere con centro x e raggio r.
Naturalmente si può pensare ad  come ad un insieme costituito di infiniti punti ognuno dei quali è dotato di un proprio intorno U(x) o, per meglio dire, di una famiglia di intorni avente le seguenti proprietà:
1) x Î U(x) ossia x appartiene al suo intorno
2) se ad una stessa x, corrispondono 2 intorni, allora l´intersezione di questi 2 intorni è ancora un intorno di x
3) se un punto y Î all´intorno di x allora esiste un intorno di y completamente contenuto nell´intorno di x
4) se 2 punti sono separati, (come ad esempio in Q) allora sono separati anche i loro intorni.
Se in un insieme sono rispettate tutte queste proprierà, tale insieme viene definito spazio topologico.
Oltre ad Rn sono spazi topologici anche i seguenti:
Â* = Ân È { - ¥ } È { + ¥ )
Si noti che si tratta di un insieme ordinato e che - ¥ e + ¥ non sono dei ni bensì soltanto dei simboli rappresentanti dei concetti. È ancora possibile parlare di intorni ed in particolare si afferma:
1) L´ intorno di x rimane inalterato ossia è l´intervallo aperto ( x - Î , x + Î ) sulla retta orientata rappresentante Â.
2) L´intorno di +¥ è la semiretta che va da x a +¥ con quest´ultimo punto interno a chiusura della intervallo.
3) L´intorno di -¥ è la semiretta che va da x a -¥ con quest´ultimo punto interno a chiusura della intervallo.
![]() = Ân È { ¥ }
= Ân È { ¥ }
Esso può essere pensato come una retta che viene presa per i due lembi e congiunta in un punto che chiameremo ¥.
Proprio questa descrizione ci porta a dire che non è un insieme ordinato, è come una ruota dove non si sà chi è prima.
17) Classificazione dei punti:
Si abbia un insieme E in Ân , diremo che tutto ciò che non è in E , si trova nel complementare di E ossia CE.
All´ interno di E si distinguono le seguenti categorie di punti:
Punto interno Þ Un punto si dice interno ad E se il suo intorno con raggio Î > 0 è interamente contenuto in E . L´insieme dei punti interni di E viene indicato con ![]() .
.
(a,b) tutti i punti sono interni.
[a,b) tutti i punti sono interni tranne a
Punto di Frontiera Þ Un punto si dice di frontiera se nel suo intorno vi sono contenuti sia elementi di E che di CE. L´insieme dei punti di frontiera di E viene indicato con ![]() .
.
(a,b) tutti i punti sono di frontiera
[a,b) tutti i punti sono di frontiera
(a,b] tutti i punti sono di frontiera
Punto Esterno Þ Un punto si dice esterno ad E se il suo intorno con raggio Î > 0 è interamente ontenuto in CE.
Punto di accumulazione Þ Un punto interno o di frontiera si dice di accumulazione per E se nel suo intorno avente raggio e > 0 vi sono infiniti punti di E. L´insieme dei punti di accumulazione di E viene indicato con ![]() .
.
Ed il suo inverso
Punto isolato Þ Ogni punto nel cui intorno non ci sono infiniti punti di E.
Sono punti che necessariamente appartengono alla frontiera di E, si pensi alla serie seguente: ![]() essa tende a 0 ma non ci arriva mai quindi 0 è un punto di accumulazione che non appartiene ad E e gli elementi di E sono tutti punti isolati.
essa tende a 0 ma non ci arriva mai quindi 0 è un punto di accumulazione che non appartiene ad E e gli elementi di E sono tutti punti isolati.
In generale il dubbio è che ci siano o meno punti interni nell´insieme, e se ci sono il dilemma successivo è capire se siano di accumulazione o meno.
Viceversa i punti di frontiera sono sempre presenti in qualunque insieme ma non necessariamente essi sono dei punti di accumulazione.
In riferimento ai limiti vengono introdotti anche i seguenti concetti di topologia:
Intorno destro Þ L´intorno destro del punto x0 non è che l´intervallo [ x0 , x0 + d) con d > 0
Intorno sinistro Þ L´intorno sinistro del punto x0 non è che l´intervallo ( x0 + d , x0] con d > 0
Punto di accumulazione destro Þ Un punto x0 si dice di accumulazione destro se nel suo intorno destro vi è almeno un punto della insieme diverso da x0.
Punto di accumulazione sinistro Þ Un punto x0 si dice di accumulazione sinistro se nel suo intorno sinistro vi è almeno un punto della insieme diverso da x0.
18) Insiemi aperti, chiusi, nè aperti nè chiusi, aperti e chiusi:
In funzione dello spazio topologico nel quale si calano (ossia del tipo di punti di cui sono formati) gli insiemi possono essere suddivisi nelle 3 seguenti categorie:
Insiemi Aperti Þ Sono insiemi costituiti da tutti punti interni (ossia con intorno completamente contenuto in E)
(a,b) è un insieme aperto in quanto sono tutti punti interni.
Insiemi Chiusi Þ Sono insiemi non aperti. In generale, ogni insieme costituito da un n° finito di elementi è chiuso.
In particolare un qualsiasi insieme E contenuto in Rn è chiuso.
{ a } è un insieme chiuso in quanto il suo intorno non contiene nessun altro punto quindi non può essere punto interno di E.
Insiemi nè aperti nè chiusi Þ Sono insiemi che dà un lato sono aperti e dalla altro lato sono chiusi
[a,b) non è aperto perchè a non ha intorno completamente contenuto in E e d´altro canto non è nemmeno chiuso in quanto b è punto di frontiera anche per CE che quindi non può essere aperto.
Insiemi aperti e chiusi Þ Gli unici insiemi che sono sia aperti che chiusi sono {0}= insieme vuoto ed Ân,
entrambe aperti in quanto costituiti da tutti punti interni ma essendo uno il complementare della altro allora uno dei 2 deve essere anche chiuso in quanto altrimenti ci manda in aria tutta la teoria secondo la quale se un insieme non è aperto allora è chiuso.
Dimostriamo ora in italiano le seguenti affermazioni:
1) E è chiuso
2) ¶E Ì = E
3) ogni punto di accumulazione di E appartiene ad E.
1 dimostra 2
Vogliamo dimostrare che la frontiera di E è contenuta o è eguale ad E, partiamo affermando che un punto appartenente alla frontiera di E può essere o isolato, ed in tal caso appartiene ad E oppure può essere un punto di accumulazione,ma un punto di accumulazione che stà sulla frontiera di E , stà anche sulla frontiera di CE , ma essendo E chiuso, come afferma il punto 1, allora il punto x non può appartenere al CE e pertanto x Î E.
2 dimostra 3
Vogliamo dimostrare che ogni punto di accumulazione di E appartiene ad E. Partiamo dalla ipotesi che i punti della frontiera di E appartengano ad E , quindi se x è un punto di accumulazione di E, se stà sulla frontiera, per quanto appena affermato, appartiene ad E, mentre se è punto interno di E, non può che appartenere ad E.
3 dimostra 1
Vogliamo dimostrare che E è chiuso cioè che contiene punti che non sono completamente contenuti in E, lo facciamo dimostrando che CE contiene solo punti interni e pertanto è aperto. Prendiamo x ÎCE e diciamo che se il suo intorno contenesse punti di E allora potrebbe definirsi punto di accumulazione per E, ma 3) ci dice che un punto di accumulazione di E Î ad E pertanto non può appartenere alla frontiera di E. Dunque se x Î CE , deve esserne suo punto interno ma se è punto interno allora CE è aperto e pertanto E è chiuso.
Chiusura di E Þ Si denomina con questo termine l´unione di E con la sua frontiera ¶E e si indica con il simbolo ![]() .
.
Si denomina chiusura per via del precedente teorema che ci dice che E è chiuso se e solo se la frontiera di E è contenuta o è eguale ad E.
19) Limiti:Finora abbiamo parlato di operazioni insiemistiche, ora passiamo a dedicarci al comportamento delle funzioni, iniziamo individuando alcune caratteristiche tipiche delle funzioni applicate all´insieme X ed avente valori in Rn
20) Funzioni limitate:Una funzione avente Dominio X e codominio Ân con insieme di esistenza A ed immagine f (A)si dice limitata se esiste in Ân un n° reale M tale che || f(x) || < = M , " x ÎA
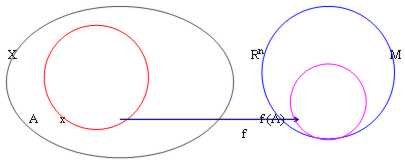
Tuttavia i casi di esempio sono al solito n = 1 (retta) ed n = 2 (piano).
In  accade il seguente:
una funzione è limitata superiormente in A se $ M Î Â tale che f (x) < = M " x Î A
una funzione è limitata inferiormente in A se $ N Î Â tale che f (x) > = N " x Î A
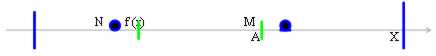
Questa funzione si dice limitata in quanto è limitata sia superiormente che inferiormente. Da questo deriva che f(A) è un insieme limitato superiormente ed inferiormente e che quindi per la proprietà di completezza (Se un insieme A è limitato superiormente(inferiormente) ossia ammette almeno un maggiorante(minorante), allora esso ammette anche estremo superiore(inferiore) ossia esiste un maggiorante(minorante) che precede(segue) gli altri) ammette estremo superiore ed inferiore.
Nel nostro caso l´estremo superiore esiste ed è M, a patto che rispetti le caratteristiche della estremo superiore:
1) " x Î A : f(x) < = M
2) "Î > 0 : f(x) > M - Î
ossia l´estremo superiore deve essere il più piccolo dei maggioranti e per quanto piccolo si prenda un Î e lo si sottragga ad M, M non è più maggiorante perchè c´è un f(x) che è più grande.
Se non ci fosse stato M avremmo assunto sup A = ¥
Nel nostro caso l´estremo inferiore esiste ed è N, a patto che rispetti le caratteristiche della estremo inferiore.
1) " x Î A : f(x) > = N
2) "Î > 0 : f(x) < N + Î
ossia l´estremo inferiore deve essere il più grande dei minoranti e per quanto piccolo si prenda un Î e lo si sommi ad N, N non è più minorante perchè c´è un f(x) che è più piccolo.
Se non ci fosse stato N avremmo assunto Min A = -¥
Avremmo invece parlato di massimo o di minimo globale se M o N rispettivamente avessero fatto parte di A
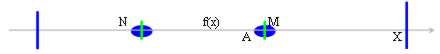
Questa volta il teorema della completezza ci è inutile infatti quando sappiamo che f(x) è limitata superiormente(ossia ha dei maggioranti), possiamo dire che f(x) ammette estremo superiore ma non sappiamo se questo estremo sia il massimo, analogamente per il minimo.
Se invece ora passiamo al caso n = 2 evidenziamo il seguente:
Passiamo ora a descrivere un concetto fondamentale nella trattazione dei limiti, la dipendenza del nostro studio non dall´insieme d´esistenza bensì dal codominio ed in particolare dall´immagine. Spesso ci troveremo ad osservare delle curve del genere ed a prendere intorni di un punto nell´ I.E. ma questi intorni sono importanti solo se considerati come proiezione sulla curva del vero intorno scelto arbitrariamente nella immagine.
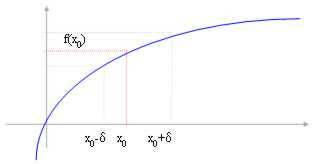
Si noti che in questo caso la funzione non ha Inf f(A) pertanto assumeremo per default inf f = - ¥
analogamente sembra non avere Sup f(A) pertanto assumeremo per default sup f = + ¥
Definiamo pertanto:
* massimo relativo un punto della immagine dove f(x0) > = f(x) con x Î intorno di x0
* massimo relativo forte un punto della immagine dove f(x0) > f(x) con x Î intorno di x0
* massimo assoluto un punto della immagine dove f(x0) = M cioè Sup A e f(x) =< M cioè Sup A
* minimo relativo un punto della immagine dove f(x0) < = f(x) con x Î intorno di x0
* minimo relativo forte un punto della immagine dove f(x0) > f(x) con x Î intorno di x0
* minimo assoluto un punto della immagine dove f(x0) = N cioè Inf A e f(x) =< N cioè Inf A
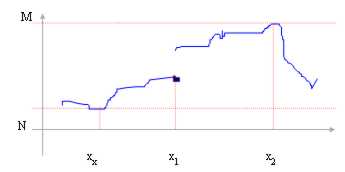
In questo esempio:
M = Sup f(A)
N = Inf f(A)
x2 è punto di massimo globale o assoluto
x0 è punto di minimo globale o assoluto
x1 è punto di minimo locale in quanto nell´intorno dx f(x1)<f(x) e nell´intorno sx ha valori minori f(x1)=f(x)
Si noti in generale nelle definizioni che l´immazine si chiama m.... mentre la corrispondente x si chiama punto di m.... .
21) Limite di funzione reale di una variabile reale:Il limite è uno strumento, una operazione che si propone di risolvere particolari preoblemi delle funzioni come :
* La discontinuità (asintoti)
* Il comportamento della funzione per valori molto grandi o molto piccoli
quindi riassumendo il limite non è altro che una ricerca dei punti di accumulazione della funzione ossia di quei punti in cui l´immagine si addensa in intorni molto piccoli di un valore che definiremo limite l.
La definizione di limite ci ho messo circa 2 settimane per capirla in quanto intrinsecamente espressa male, sostanzialmente però è la seguente:
Si osserva la equazione della funzione e si determina che per determinati valori della x chiamati x0 , la funzione non è definita. Da questa osservazione passiamo a dedurre sul grafico quale era il valore della funzione nei punti immediatamente precedenti e seguenti x0, se tali valori sembrano ammassarsi verso un punto di accumulazione, allora diciamo che tale punto è il limite della funzione per x ® x0 a patto però che :
Se prendiamo un intorno V di l grande quanto una inezia, ad esempio l´ intorno (l - e , l + e) con e > 0 , dobbiamo riuscire a trovare un intorno di x0 (con x0 escluso) ad esempio (x-d , x+d) con d > 0, per il quale la funzione sia compresa nell´intorno V di l.
Tale limite si chiama limite di f(x) per x che tende ad x0.
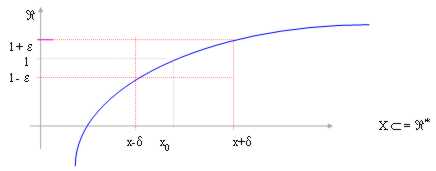
In questo caso il limite è sicuramente l in quanto la funzione per x-d <x < x+d è sicuramente contenuta nell´intorno di l e si può anche osservare che l stesso è un punto di accumulazione per x®x0. Cioè per x®x0 la funzione è definitivamente compresa nell´intorno di l.
Dato che l Î Â diremo anche che la funzione ammette limite finito per x Þ x0.
Se x0 fosse stato +¥ allora avremmo preso l´intervallo nel dominio (m , +¥).
Se x0 fosse stato -¥ allora avremmo preso l´intervallo nel dominio (-¥ , m).
Se f(x) ® ¥ per x®x0 si dice che la funzione è un infinito.
Se f(x) ® 0 per x®x0 si dice che la funzione è un infinitesimo e si scrive o(1).
Si tenga bene presente che non ci interessa cosa fà la funzione in x0 , tanto che escludiamo tale punto dalla definizione di limite, ciò appunto per risolvere casualità dove la funzione non è definita per un determinato punto.
In questo caso in cui la funzione è tutta nell´intervallo [ l , l + e)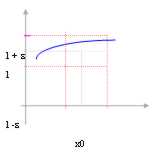
Si dice che la funzione è limitata per eccesso e si scrive:
![]()
In questo caso in cui la funzione è tutta nell´intervallo [ l + e , l ) 
Si dice che la funzione è limitata per difetto e si scrive:
![]()
In questo caso in cui la funzione è tutta nell´intervallo (x0 - d , x0) 
Si dice che la funzione ammette solo limite sinistro e si scrive:
![]()
In questo caso inoltre si dice che la funzione è un infinito.
In questo caso in cui la funzione è tutta nell´intervallo [x0 , x0 + d) 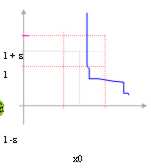
Si dice che la funzione ammette solo limite destro e si scrive:
![]()
In questo caso inoltre si dice che la funzione è un infinito.
22) Proprietà dei limiti:
Dei limiti conosciamo le seguenti proprietà che possono sembrare banali in quanto intuitive, ma nascondono molto più lavoro di dimostrazione di quanto sembri:
Permanenza del segno
Questa proprietà afferma che se noi sappiamo che il limite per x ® x0 ha una determinata proprietà ( ad esempio è maggiore di 0), allora possiamo dire che anche f(x) per x ® x0 ha quella determinata proprietà.
Si noti bene che non è sempre vero il contrario, ossia se noi sappiamo che la funzione per x ® x0 ha definitivamente una proprietà in quell´intorno, allora non possiamo dire che anche il limite possiede quella proprietà o quanto meno non in maniera forte, ossia si faccia l´esempio della funzione x2 > 0 , essa ha come limite 0 ma 0 non è > 0 , cioè noi sappiamo che la funzione è definitivamente > 0 ma il limite può essere > = 0.
La situazione si può risolvere prendendo un intorno di l nel quale la funzione è definitivamente positiva.
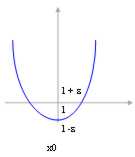
Si tratta cioè di prendere e = l - d pertanto 0 < l - ( l - d) < l e dunque f(x) è
definitivamente positiva e lo è anche il suo limite.
Ma questo unicamente se il limite è > 0 quindi non è questa la figura adatta.
Dimostrazione:
Basta porre e = l ed allora l´intorno considerato diviene ( 0 , 2l ) ed in questo intorno la funzione non può che essere positiva.
Il limite , se esiste, è unico.
Si dimostra con gli intorni, affermando che 2 limiti diversi per x ® x0 hanno 2 intorni V1 e V2 ai quali corrispondono 2 intorni di x0 , ma l´intersezione di 2 intorni è ancora un intorno di x0 mentre l´intersezione di V1 e V2 è vuota, il che è un assurdo quindi i due limiti coincidono ed il limite è unico.
Se esiste il limite allora la funzione è definitivamente limitata ( ammette sup f(x) ).
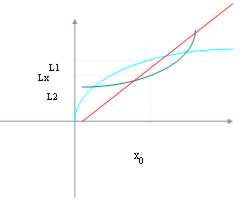
23) Teorema del confronto:Avendo 2 funzioni, f(x) e h(x) delle quali conosciamo i limiti l1 ed l2 ed una funzione g(x) della quale non conosciamo il limite ma sappiamo che nell´intorno di x0 è compresa tra f(x) e h(x) allora possiamo dire che anche il limite di g(x) è compreso tra l1 ed l2.
Tutto questo assume dimensioni eccezionali allorchè l1 = l2 infatti in questo caso deve essere forzatamente l1 = l2 = l3 e quindi siamo riusciti a determinare il limite di una funzione che non avremmo saputo determinare diversamente.
Chiaramente affinchè questa relazione sia valida l´intorno deve essere il più piccolo possibile.
A questo teorema dobbiamo il limite ![]() =1 per x ® 0 .
=1 per x ® 0 .
Nella trattazione di limiti in cui x0 può appartenere ad Â* si possono incontrare le seguenti situazioni, parte delle quali sono risolubili, ossia:
La seguente risolve il caso +¥ + l accertandosi che l stesso non valga -¥ nel qual caso sarebbe indeterminata ¥ -¥.
1) +¥ + f(x) limitata inferiormente (possiede un InfX) = +¥
La seguente risolve il caso -¥ + l accertandosi che l stesso non valga +¥ nel qual caso sarebbe indeterminata -¥ +¥.
2) -¥ + f(x) limitata superiormente (possiede un SupX) = -¥
La seguente risolve il caso +¥ - l accertandosi che l stesso non valga +¥ nel qual caso sarebbe indeterminata +¥ -¥
3) +¥ - f(x) limitata superiormente (possiede un SupX) = +¥
La seguente risolve il caso -¥ - l accertandosi che l stesso non valga ¥ nel qual caso sarebbe indeterminata -¥ + ¥
4) -¥ - f(x) limitata inferiormente (possiede un InfX) = -¥
5) +¥ * l = +¥
6) +¥ * -l = -¥
7) -¥ * l = -¥
8) -¥ * -l = +¥
9) 0 * l = 0
10) 1 / 0+ = ¥ 
11) 1 / 0- = -¥
tutti i casi che non rientrano in questi si chiamano forme indeterminate e si risolvono con uno dei seguenti artifixi:
1) 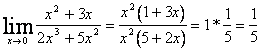
2) 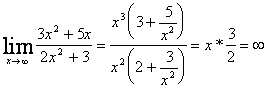
3) Laddove compaiano delle frazioni è possibile la razionalizzazione del numeratore.
25) Limite di funzioni composte:
Se abbiamo una funzione f da X avente immagine in un altro insieme Y e supponiamo che questa immagine contenga anche il limite della funzione l per x ® x0 . Si abbia poi una funzione g(y) che associa all´immagine f(X) un valore k in un altro insieme per y®l allora è possibile affermare che il limite per x®x0 di g(f(x)) è k.
Si noti che tassativamente deve essere f(x) ¹ l così come era x ¹ x0.

La dimostrazione procede a ritroso rispetto al disegno, ossia si afferma che per ogni intorno W(k) esiste un intorno V(l) per il quale la definizione di limite sia rispettata, analogamente per tale intorno V(l) esiste un intorno U(x0) per il quale la definizione di limite sia rispettata. È in corrispondenza di questo intorno che è rispettato il limite della funzione composta.
Si osserva poi che questa peculiarità è di grande aiuto nel momento in cui comprendiamo di poterci ricondurre ad un limite notevole semplicemente effettuando un cambio di variabile, il limite però a questo punto cambia, facendo un esempio:
![]() poniamo
poniamo ![]() ed abbiamo
ed abbiamo ![]()
26) Limiti di funzioni monotone:
Per le funzioni monotone, il calcolo del limite per x ® x0 è agevolato in quanto tale limite corrisponde con l´ Inf della funzione o con il Sup della funzione stessa a seconda dei seguenti casi:
1)
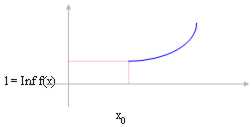 Se la funzione è crescente e noi consideriamo solo l´intorno
Se la funzione è crescente e noi consideriamo solo l´intorno
destro di x0 Î Â* allora il limite per x ® x0 corrisponde
l = Inf f(x) con l´Inf della funzione nell´intervallo (x0 , + ¥).
x0
2)
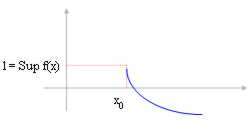 Se la funzione è decrescente e noi consideriamo solo l´intorno
Se la funzione è decrescente e noi consideriamo solo l´intorno
destro di x0 Î Â* allora il limite per x ® x0 corrisponde
l = Sup f(x) con il Sup della funzione nell´intervallo (x0 , + ¥).
x0
3)
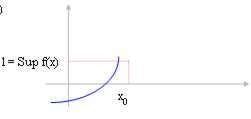 Se la funzione è crescente e noi consideriamo solo l´intorno
Se la funzione è crescente e noi consideriamo solo l´intorno
sinistro di x0 Î Â* allora il limite per x ® x0 corrisponde
l = Sup f(x) con il Sup della funzione nell´intervallo (-¥ , x0).
x0
Si dimostra osservando che si possono presentare i 2 casi seguenti:
A) l Î Â
per le proprietà della estremo superiore:
a) " x Î X Ç (- ¥, x0) : f(x) < = l
b) "Î > 0 $ xÎ Î X Ç (- ¥, x0) : f(xÎ) > l - Î
Inoltre essendo la funzione crescente possiamo dire: l - Î < f(xÎ) < l = Sup f(x)
B) l = +¥
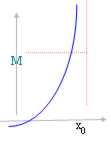
f(x) > M " x Î X Ç (- ¥, x0) e pertanto il limite è +¥.
4)
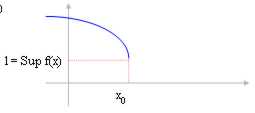 Se la funzione è decrescente e noi consideriamo solo l´intorno
Se la funzione è decrescente e noi consideriamo solo l´intorno
sinistro di x0 Î Â* allora il limite per x ® x0 corrisponde
con l´Inf della funzione nell´intervallo (-¥ , x0).
Da queste osservazioni sui limiti di funzioni monotone nè derivano analoghe sui limiti di potenze, esponenziali e logaritmi e tutti finalizzati alla risoluzione di limiti del tipo ![]() .
.
Una successione non è che un tipo particolare di funzione da À in  che associa cioè ad ogni n° naturale un valore in  secondo una legge imposta dalla successione stessa. Essa non ha punti di accumulazione in À se non +¥.
A seconda di come si comporta la funzione verso questo punto di accumulazione si distinguono i seguenti 3 casi :
Successione convergente: Al tendere di n verso +¥ la successione si stabilizza verso un valore reale l.
La definizione di limite in questo caso ci dice che " Î > 0 a partire dal n° N dal quale la successione si stabilizza ad ogni n corrisponde un valore della funzione che discosta dal limite l meno di Î.
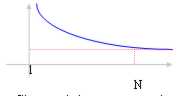
Si osservi che una successione convergente è anche limitata ( ||f(x)|| < = M) in base a quanto già affermato quale conseguenza che l Î Â che come sappiamo è un campo ordinato.
Non è però sempre vero che una successione limitata sia anche convergente, vi sono funzioni si limitate tra 2 valori ma che oscillano in continuazione tra uno e la altro, pertanto sono irregolari.
Le funzioni monotone come quella della figura oltre ad essere convergenti sono anche limitate, il limite è finito se la successione è limitata altrimenti il limite è +¥.
Se la successione tende ad un limite l > 0 allora è anche essa definitivamente >0 per n ® +¥, non è invece vero il contrario ossia se la successione è definitivamente >0 , non è detto che lo sia anche il suo limite il quale potrebbe essere cioè = 0.
In generale, possiamo dire che se per n ® +¥ tre successioni hanno la seguente relazione d´ordine, an [ bn [ cn e sia an che cn tendono al limite l , allora anche bn tende al limite l.
Successione divergente: Al tendere di n verso +¥ la successione diverge verso ±¥.

Il limite, nel caso la successione diverga verso +¥ è lo stesso +¥
Successione irregolare: Al tendere di n verso +¥ la successione non si stabilizza verso alcun valore bensì oscilla.
28) Teorema “ponte” e non esistenza dei limiti :
Esiste un teorema che rappresenta la congiunzione tra le considerazioni fatte sui limiti delle successioni e quelle fatte sui limiti dellle funzioni, non a caso questo teorema si chiama “ponte”. Esso afferma:
Il limite per x ® x0 di una funzione f(x) è l Û
" successione sulle ascisse che tende a x0 per n ® ¥ , il limite della funzione della successione è l.
In pratica noi abbiamo una successione sulle ascisse che tende ad x0, applichiamo la funzione ai termini di questa successione e troviamo che il limite di questa funzione trovata è lo stesso l che avevamo trovato per x ® x0 .
Questo teorema si dimostra scindendo il Û nelle 2 componenti e dimostrando separatamente:
Dimostriamo ora che se ![]() Þ
Þ ![]()
Si dimostra osservando che se an ® x0 allora a partire da un certo valore N in poi la definizione di limite che è a sinistra verrà rispettata in quanto la successione cade nell´intorno di x0 e la corrispettiva funzione, nell´intorno di l.
Dimostriamo ora che se ![]() Ü
Ü ![]()
Si dimostra per assurdo affermando che quella a sinistra sia vera ma sia falsa la definizione di limite a destra.
Negare la definizione di limite equivale a dire che esiste un e > 0 tale che " d >0 esiste un xd che sia contenuto nell´intorno di x0 ma il corrispondente valore della funzione esce fuori dall´intorno del limite l.
Una volta affermato questo possiamo assegnare ad xd i valori dei termini della successione ed ossrevare che quindi la successione è contenuta nell´intorno di x0 ma la funzione corrispondente non è contenuta nell´intorno di l, pertanto vien contraddetto il 2° membro della equazione essendo partiti dalla negazione del 1° membro, pertanto, l´equazione così come è scritta è corretta.
La maggiore applicazione di questo teorema è nella negazione della esistenza dei limiti, infatti si osserva che se 2 successioni tendono entrambe ad x0 per n ® ¥ ma la funzione applicata a queste 2 successioni dà 2 limiti diversi, allora il limite non esiste.
In pratica per negare l´esistenza di un limite, occorre:
1) trovare 2 successioni che per n® ¥ tendano ad x0
2) Verificare che il limite della funzione applicata alla successione, per n ® ¥ sia diverso per le due successioni.
29) Infiniti, infinitesimi e confronti:Vi sono dei casi in cui il calcolo dei limiti conduce a forme indeterminate, ad esempio: 0 / 0 oppuranche ¥ / ¥, in queste occasioni può essere utile al fine del calcolo del limite, confrontare con quale velocità le due funzioni divengono infinitesime o infinite, ossia se una delle 2 è più lenta rispetto alla altra per cui anche se entrambe vanno a 0 si può dire che prevalendo una , il valore della altra non è significativo ed il limite pertanto è 0 oppure ±¥. Analogamente se le 2 funzioni sono infinite, potremmo dire che una delle 2 va ad ¥ più rapidamente della altra e pertanto il valore della altra può essere trascurato ed il limite assume quindi il valore 0 o ±¥ a seconda dei casi.
Funzione infinitesima : 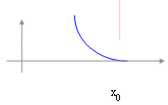 è una funzione che per x ® x0 tende a 0 .
è una funzione che per x ® x0 tende a 0 .
Funzione infinita : 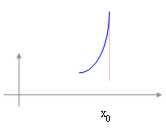 è una funzione che per x ® x0 tende ad ¥.
è una funzione che per x ® x0 tende ad ¥.
x0
Si distinguono i 2 seguenti casi:
1) Le due funzioni sono entrambe infinitesime per x ® x0 allora il limite del rapporto f(x) / g(x) vale:
0 nel caso f(x) sia infinitesima di ordine superiore rispetto a g(x) ossia tenda a 0 più rapidamente.
Si pensi al caso ![]() dove (1 - cos2x) è un infinitesimo di ordine superiore rispetto ad x cioè tende a 0 più rapidamente e riporta il limite ad un caso 0 / x = 0.
dove (1 - cos2x) è un infinitesimo di ordine superiore rispetto ad x cioè tende a 0 più rapidamente e riporta il limite ad un caso 0 / x = 0.
l Î Â \{0} se le due funzioni sono infinitesime dello stesso ordine.
Si pensi al ![]()
± ¥ nel caso f(x) sia infinitesima di ordine inferiore rispetto a g(x) ossia tende a 0 più lentamente.
Si pensi al ![]() dove xa è un infinitesimo di ordine inferiore rispetto a sinx pertanto prevale l´effetto di quest´ultimo
dove xa è un infinitesimo di ordine inferiore rispetto a sinx pertanto prevale l´effetto di quest´ultimo
non esiste il limite in Â*
Si pensi al caso ![]() limite che non esiste in quanto la funzione oscilla continuamente secondo la legge del seno a ridosso della origine.
limite che non esiste in quanto la funzione oscilla continuamente secondo la legge del seno a ridosso della origine.
2) Le due funzioni sono entrambe infinite per x ® x0 allora il limite del rapporto f(x) / g(x) vale:
0 nel caso f(x) sia infinita di ordine inferiore rispetto a g(x) ossia tenda a ¥ più lentamente.
Si pensi al caso ![]() dove xa è un infinito di ordine inferiore rispetto ad ax cioè tende a ¥ più lentamente riporta il limite ad un caso x / ¥ = ¥.
dove xa è un infinito di ordine inferiore rispetto ad ax cioè tende a ¥ più lentamente riporta il limite ad un caso x / ¥ = ¥.
l Î Â \{0} se le due funzioni sono infinite dello stesso ordine.
Si pensi al ![]()
± ¥ nel caso f(x) sia infinita di ordine superiore rispetto a g(x) ossia tende a ¥ più velocemente.
Si pensi al ![]() dove il logaritmo è un infinito di ordine superiore rispetto all´esponenziale, pertanto prevale l´effetto del logaritmo.
dove il logaritmo è un infinito di ordine superiore rispetto all´esponenziale, pertanto prevale l´effetto del logaritmo.
non esiste il limite in Â*
Si pensi al caso ![]() limite che non esiste in quanto la funzione oscilla continuamente secondo la legge del seno andando verso ¥.
limite che non esiste in quanto la funzione oscilla continuamente secondo la legge del seno andando verso ¥.
Si osservi che quando il limite di una funzione per x ® x0 risulta essere 0 , si dice che la funzione è un o(1) ad indicare che vale una inezia, tuttavia è una quantità che va considerata in quanto forse inutile nelle somme ma determinante nei prodotti, capace di annullare anche un gigante.
Un altro utilizzo della ” o piccolo” è appunto il limite del rapporto tra 2 funzioni, ![]() .
.
Se f(x) = g(x) = infinitesima e ci rendiamo conto che f(x) tende a zero più rapidamente che non g(x) possiamo dire che f(x) = o(g(x)) ossia che f(x) è un infinitesimo di g(x).
In modo del tutto analogo,
Se f(x) = g(x) = infinita e ci rendiamo conto che f(x) tende a +¥ più rapidamente che non g(x) possiamo dire che f(x) = o(g(x)) ossia che f(x) è un infinito di ordine inferiore rispetto a g(x).
Le potenzialità di questo strumento però vengono esaltate allorquando nel corso del calcolo di alcuni limiti si potrà sostituire qualche espressione di limite notevole con il suo valore + o(1) ad indicare che per x ® x0 il valore è quello ma si deve sempre tener conto di un infinitesimo.
31) O(.) :Si osservi che quando il limite di una funzione per x ® x0 risulta essere l Î Â , si dice che la funzione è un O(1) ad indicare che assume un valore limitato.
Un altro utilizzo della ” O grande” è appunto il limite del rapporto tra 2 funzioni, ![]() .
.
Se f(x) = g(x) = infinitesima e ci rendiamo conto che il rapporto tende ad un limite finito possiamo dire che f(x) = O(g(x)) ossia che f(x) è in relazione finita con g(x).
In modo del tutto analogo,
Se f(x) = g(x) = infinita e ci rendiamo conto il rapporto tende ad un limite finito possiamo dire che f(x) = O(g(x)) ossia che f(x) è in relazione finita con g(x).
Si osservi che quando il limite di un rapporto tra funzioni per x ® x0 , ![]() con f(x) = g(x) = infinitesime o infinite si dice che f(x) è asintotica a g(x) , in simboli f(x) ~ g(x).
con f(x) = g(x) = infinitesime o infinite si dice che f(x) è asintotica a g(x) , in simboli f(x) ~ g(x).
Nel caso le 2 funzioni siano dello stesso ordine allora si dice che sono asintotiche a meno di una costante moltiplicativa.
32) Infiniti ed infinitesimi campione:Talvolta potrà risultare utile individuare l´ ordine di un infinitesimo per semplificare il calcolo dei limiti, viene perciò introdotto il concetto della infinitesimo campione , ossia noi abbiamo un rapporto tra 2 funzioni di cui una , g(x) la introduciamo noi a nostro piacere e verrà definita infinitesimo campione, per conoscere l´ordine di infinitesimo della altre, f(x) ci basterà sapere a quale esponente dobbiamo elevare g(x) affinchè il rapporto abbia un limite reale per
x ® x0 ossia nella ![]() ci interessa conoscere il valore di a, esso rappresenta l´ordine di infinitesimo della f(x). Analogo discorso si fà per gli infiniti.
ci interessa conoscere il valore di a, esso rappresenta l´ordine di infinitesimo della f(x). Analogo discorso si fà per gli infiniti.
La scelta della funzione campione, g(x) avviene normalmente come segue:
infinitesimo campione: a) x - x0 se il limite è per x ® x0 ad esempio se x ® 0 allora l´infinitesimo campione è x.
b) 1/x se il limite è per x ® ±¥ ad esempio se x ® ¥ allora l´infinitesimo campione è 1/x.
Infinito campione: a) ![]() per x ® x0± ad esempio per x ® 0 g(x) =
per x ® x0± ad esempio per x ® 0 g(x) = ![]() .
.
b) x per x ® ±¥ .
Nella scelta della infinito campione si deve evitare di imporre esponenti radici per numeri negativi cambiando campione.
33) Il n° e :Abbiamo visto come si ricava il n° e , esso in particolare vale ![]() .
.
Per giungere a questo risultato, si osserva che il rapporto ![]() (dove
(dove ![]() ) per n > 2 è maggiore o uguale ad 1 cioè il numeratore è maggiore o uguale al denominatore, quindi da questo deduciamo che an è una successione limitata e crescente in quanto l´elemento successivo è maggiore della elemento precedente.
) per n > 2 è maggiore o uguale ad 1 cioè il numeratore è maggiore o uguale al denominatore, quindi da questo deduciamo che an è una successione limitata e crescente in quanto l´elemento successivo è maggiore della elemento precedente.
Si prende poi la successione ![]() , la si confronta con l´elemento precedente secondo il seguente rapporto
, la si confronta con l´elemento precedente secondo il seguente rapporto ![]() e si osserva che tale rapporto è minore o uguale ad 1 , pertanto la funzione è decrescente.
e si osserva che tale rapporto è minore o uguale ad 1 , pertanto la funzione è decrescente.
Ma lo scopo di questa seconda successione era evidenziare che an possiede un sup(an) ed il sup esiste in quanto
0 < an < bn pertanto an è inequivocabilmente limitata.
Siamo arrivati alla conclusione che e non è altro che il punto a cui tendono queste 2 successioni, si può tornare cioè a parlare del concetto di n° reale come sezione.