Champs électriques magnétiques variables et dans le temps
1) équations de maxwell dans le cas stationnaire dans le vide :
2) loi de Faraday Neumann :
Il signifie pour décrire les phénomènes dans lesquels
une variation de la période de l'écoulement du concatenato de B avec
le circuit il induit dans lui que un f.e.m. donné 
des variations de flux peut dériver d'une des causes
suivantes :
) mouvement mécanique du circuit
b) variation du champ de B dans le temps
c) variation de la géométrie du circuit
3) champ électrique en conditions non stationnaires :
En conditions non stationnaires le champ électrique n'est
pas conservativo, n'est pas en valeur plus de qui
est mais une dépendance de la variation temporelle du champ de B est
trouvée, donc comme l'intuisce de la loi de Faraday Neumann.
4) loi de Lenz :
F.e.m. que la variation est induite dans un circuit au del de della de suite l'écoulement du concatenato B est tels de l'opporsi à cette variation d'écoulement, celui est un glissera le courant induit par circuit de nel qu'il donne à endroit à un champ de B qui s'oppose à celui qu'il a produit de lui.
5) écoulement coupé :
Dans le cas dans quel B c'est constant et le circuit qu'il est dans le mouvement, l'écoulement de coupe est le traverser les murs du cylindre qui joint le circuit au temps t avec le circuit au temps t '. Il est égal à la variation de l'écoulement du circuit.
6) cause du f.e.m. induit dans le cas du circuit dans le mouvement et la source ferme :
La force de Lorentz.
7) cause du f.e.m. induit dans le cas du circuit et de la source fermes dans le mouvement :
C'est toujours la force de Lorentz, asse'à dans le mouvement choisissent un système de la référence dans lequel la source est ferme.
8) troisième équation de maxwell dans le cas non stationnaire :
Il est obtenu à partir de l'être 
sur ceci applique le théorème du rotor et
finalement l'integrandi sont égalés aux 2 membres.
9) autoindotta de f.e.m. :
Un circuit couvert du courant variable dans le temps donne
à l'endroit à la variable un champ de B également il dans le temps, une variation de l'écoulement du
concatenato de B avec le même circuit et donc pour l'indurrà un f.e.m.
soyez donc ce eu il est opposé à celui-là qui a produit
de lui.
10) coefficient de art de l'auto-portrait-induction :
En outre l'inductance est dite et s'avère être un
coefficient de la proportionnalité entre l'écoulement de B par le
circuit et le courant qu'elle a produit de B, dans les formules
a 
, mesure en Henry et est seulement dépendue des
caractéristiques géométriques.
11) coefficient de art de l'auto-portrait-induction d'un solénoïde :
12) coefficient de art de l'auto-portrait-induction bifilar d'une ligne :
étant D la distance entre les conducteurs et au faisceau
de chacun d'elles
13) coefficient de art de l'auto-portrait-induction d'un câble coaxial :
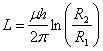
14) constante de période du circuit LR :
15) Extracorrente de l'ouverture :
Quand on ouvre un circuit en lequel une inductance est présente, la variation du courant et donc de l'écoulement est instantanée et donc pour la loi de Faraday Neumann l'élévation sera autoindotta produit de f.e.m. beaucoup qui étincellent aux têtes du commutateur peut également réussir dedans pour faire le scoccare un.
16) loi d'heureux :
Elle établit les charges Q qui entre dans un circuit
comme la conséquence d'une variation de l'écoulement de B est
eue 
.
17) coefficient d'induction mutuelle :
Quand 2 sont les circuits eus couverts du courant variable
dans le temps, le puits le courant que les glissières dans l'un des 2
produit un champ de B qui placent à un f.e.m. induit le concatena
avec l'autre circuit donnant et donc à un courant. Dans les
formules 
d'ailleurs
est eu
18) énergie possédée d'une inductance couverte du courant :
représente l'énergie possédée d'une inductance
couverte du courant I
Il est se multiplier obtenu pour Idt que l'équation les différencie d'un circuit RL avec le générateur caractérisant la densité de Lydian de l'énergie et l'intégrant entre 0 et I.
19) densité d'énergie dans un champ magnétique :
Il représente la densité actuelle de l'énergie dans une
région de l'espace dans laquelle un champ d'induction magnétique de
module de B. est présent l'intégrant sur un volume obtient est donc beaucoup de bénéfices afin de calculer le
laddove d'inductances que la méthode des écoulements est
d'application difficile.
20) courants parasites ou de Foucault :
Si dans un conducteur un champ de B est variable eue dans
le temps, s'exécutant le circuitazione et le long de de l'n'importe
quel circuit fermé étant trouve une valeur non
nulle donc à l'intérieur du conducteur circule des courants induit
parasite ou de Foucault qui détourne l'énergie au champ magnétique.
21) densité du courant de mouvement :
Le courant de mouvement vient présenté afin d'expliquer parce que si c'est appliqué le théorème du circuitazione avec une surface que les passages dans le condensateur obtient un divers résultat concernant ce qu'il serait eu avec une surface qui croise un fil du circuit cette porte au condensateur.
22) courant du mouvement :
N'importe quelle surface de S du courant du mouvement est 
le traverser un.
23) équation quarte de maxwell dans le cas non stationnaire :
Il établit la dépendance du rotor de B également de la variation temporelle du champ électrique.
Il est obtenu remplaçant la La dans
l'équation du continuità 
24) équations de maxwell dans le vide dans le cas non stationnaire :
25) équations de maxwell dans la matière dans le cas non stationnaire :
