Teoremas en los lmites
Lmites de funciones
1) oneness del lmite:
Descripcin: si 
e 
l1 = l2
si fuera l1 l2 tendran que existir alrededor de l1 y alrededor de l2 entre distinguido ellas a cul tendra que 0 corresponder el intorni 2 distinguidode x qu esa en lugar de otro PU a no suceder ya que la interseccin del intorni 2 de x0 sigue siendo una alrededor de x0 y contendr por lo menos un punto de x x0 en cunto x0 es un punto de la acumulacin (por lo tanto cada alrededor de x0 0 contiene por lo menos un punto del vario dominio Xde x). Despus de que todos por lo tanto la interseccin de 2 que el intorni no es vaco contra hicieran hiptesis.
2) teorema de la permanencia de la muestra:
Descripcin: si 
entonces f(x) > 0
definitivo para x ® x0 donde el trmino indica definitivo que la caracterstica
es vlida para cada x que pertenece por lo menos uno alrededor de x0 con x x0 .
Si 0 < l < entonces eligiendo y = l que se hace de modo que alrededor de V de l sea (0, 2l) y para esto alrededor tendremos uno alrededor de x0 en el cual la funcin se abarque entre 0 y 2l.
Ojo : el hecho de que una funcin
es > 0 no implica que l es tambin su lmite, como un ejemplo x2 es definitivo mayor de 0 para
x®0 (excluye definitivo el punto x0 = 0 donde x2 = 0) pero 
Mejora dvil: Si 0 < l < entonces eligiendo y = l - marcas de m de modo que alrededor de V de l est (m , 2l - m) y por lo tanto se puede ampliar el refrn del teorema que es vlido para cada 0 < m. < l, de que es un solo no existe alrededor pero uno para cada m elegido entre 0 existe algn y l.
3) Relazioneship entre la existencia de un lmite terminado y el limitatezza de la funcin:
Descripcin: Si para una funcin existe un lmite terminado para x®x0 que la funcin es definitivo limitada para x®x0
pero no se dice que si la funcin entonces se limita l admite un lmite terminado, pues un sgnx del ejemplo es una funcin limitada pero el lmite para x 0 no existe® .
4) teorema de la comparacin:
Descripcin: Si tengo 2 el tener de f(x) y de h(x) de las funciones el mismo lmite l para x 0® x y un tercio g(x) de la funcin se abarca definitivo entre el h(x) y el f(x) para x ® x0 entonces tambin g(x) que estira al mismo lmite l.
Para cada alrededor V de l tendr que existir alrededor de un U1 de x0 para el cual el f(x) V y uno alrededor de U2 de x0 para que el h(x)V, para cada x que pertenece a la interseccin del intorni estos 2 l sea tenido bien que es f(x) que el h(x) ellos pertenecer a V y por lo tanto tambin el g(x) que est en medio ellos abarc.
Esempio: clculo del lmite de sinx/x.
5) cunto vale el lmite del tener producto entre el f(x) que tiene lmitel 1 y el lmite l 2del g(x)
Descripcin: el f(x)*g(x) tiene como el lmite l1* l2 .
Affinch es verdad debe ser | f(x)*g(x) - l1* l2 | < y se se obtiene para irse del f(x)g(x) de la expresin con el siguiente:
1) 1 l 2 se escribeel f(x)g(x)-l 1 l 2 =f(x)g(x)-l
2) uno ensambla y quita 2 al miembro l1* g(x).
3) recogerlo es el f(x)*g(x) alcanzado de la forma - l1* l2 = el g(x)*(f(x) - l 1) l1* (g(x) - l 2)
4) se observa que ambos los trminos entre parntesis para la definicin del lmite son ms pequeos de y y que es el g(x) que posee lmite terminado un una funcin limitada por lo tanto est |g(x)| < M para x ® x0 . La desigualdad se reduce por lo tanto al forma | f(x)*g(x) - l1* l2 | < My l1*y de que dado a la confirmacin y al carcter arbitrario la tarea.
6) cunto vale tener lmite funzione1/g(x) del lmite l1 > 0
Descripcin: 1/g(x) tiene como el lmite 1/l1 .
Affinch es verdad debe ser | 1/g(x) - 1 l1 | < y se
se obtiene para irse de | 1/g(x) - 1 l1 | realizando el denominador mnimo del comun que
da 
de nuevo al numerador de 2 a miembro resulta
ms pequeo y para de la
definicin del lmite mientras que al denominador, en la virtud del
teorema de la permanencia de la muestra, nosotros saben que, tener
lmite positivo del g(x), l es seguro que g(x) > m > 0 para x®x0 por lo
tanto que podemos escribir 
en cunto no puede ser
cancelado el denominador y por lo tanto a travs y podemos hacer pequeo cunto
deseamos la diferencia entre el lmite y la funcin.
7) debajo de el cual condiciona es posible calcular el lmite de una funcin compuesta
Descripcin: Si 
y
f(x) l definitivo para x0®x
y
si 
entonces se tiene eso 
Se demuestra al revs que afirma que un W de k existe alrededor para cul existe una alrededor de V de l yo que elementos y sean tal que el g(y) l est abarcado en W. Entonces se termina otro paso al revs para encontrar uno alrededor de x0 compuesto de x tales que el f(x) tiene valores en todo el V a excepcin de l, tales alrededor de los hallazgos que la interseccin en medio alrededor de U1 de x0 compuso de x tales que el f(x) V y alrededor de U2 de x0 compuso de todo el x para el cual el f(x) l.
8) consideraciones en los lmites de las funciones montonas:
Descripcin: un monotona de la funcin admite siempre el lmite y en detalle coincide con el f(x) de Sup si la funcin es crescent y consideramos alrededor de la izquierda de x0 , mientras que l coincide con el f(x) de los Inf si la funcin es crescent y consideramos experto de x alrededorde 0.
Para demostrar que si x entonces est aumentando el lmite es el Sup si consideramos alrededor de la izquierda de los mediosde x 0 de considerar ambos los casos posibles, eso est definiendo Sup f: = l que se tiene:
a) l "
Para la definicin del extremo avanzado se tiene:
* el f(x) l abarc "x en medio - y xo
* cada para y > 0 existe xy tal que el f(x) y > l y por lo tanto l no es un avanzado ms extremo
Siendo la funcin de aumento tendremos evidentemente que " x abarcado entre xy y x0 se tiene que el ly < el f(x) l que es l sea el lmite de f para x que estire a x0.
b) l =
La f en este caso que es no limitado advancedly por lo tanto nosotros tendr que tomar como el valor M de la referencia una de la funcin y decir que para el x a la derecha asociadadel x M a punto M puesto que la funcin est aumentando tiene que el f(x) > M y por lo tanto el lmite est . Si la funcin nula no haba sido crescent habramos podido decir.
Lmites de sucesiones a los valores en "
9) una sucesin convergente es limitada.
Puesto que una sucesin no es que una funcin particular, l sigue eso para ella vale el teorema 29) segn el cual si para una funcin la funcin existe un lmite terminado parax®x 0 es definitivo limitado para x®x0 ser tenido por lo tanto que para la n mayor de una N segura, | a n | M0 que se comporta de extremo avanzado mientras que para la n abarcada entre 0 y N tendrn que existir un mximo M1 para | a n | en de cunto representan un sottoinsieme terminado ". Despus de que todo por lo tanto la sucesina n sea limitado del mximo entre M0 y M1 .
10) un monotona limitado de la sucesin y es convergente.
11) puente del teorema entre los lmites de funciones y los lmites de sucesiones:
Descripcin: 
> 
" sucesina n a los valores en X \ {x0}y convergente a x0
Teniendo que valer 1 0 el miembro entonces tomado y > 0 existir d > tales que para cada x ese TOS sea distante de x0
0<|x - x0| < d se tiene eso | f(x)-l |< y y puesto que la sucesina n converge a x0 , despus existir un valor tal N que " n > N se tenga eso | a n - x0 | < d y por lo tanto ser tenida eso | f(an) - l | < y para cada n > N.
se procede que niega a 1 el miembro y que obtiene que
tambin 2 el miembro es falsos, en detalle la negacin que afirma
que $ y tal que para cada d > 0 x dexiste X tales que 0 < | xd - x0 | < d e | f(xd) - l | y . A este punto se
hace para estirar como un ejemplo d a 0 dandogli valora progresivamente 1, el
1/2, 1/3..., 1/n y para cada d est el valor encontrado xd para el cual | f(x) - l | y . Tenemos despus
todo de creado una sucesin que estire a x0 pero que imagen no estire a l todo mientras que
la consecuencia de la hiptesis absurda los comienza eso 
.
12) demuestra que 
" a", a > 1
Aprovechndose del puente del teorema podemos en
lugar de otro demostrar que la " sucesin bn ®
tiene
che 
. En hecho:
el trmino pasado se reduce a 0 * a = 0 en la virtud 
del y por lo tanto se demuestra eso .
Para demostrar que es necesaria traerlo
detrs 
a la forma que demostraremos para ser ugule
a 0 para n ® , se es el recoger obtenido como la
energa 2a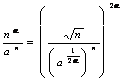 
. Para
demostrar finalmente que ® 0 por x ® est colocado h = a - 1 y disuguaglia con Bernoulli
entonces del teorema del desume de la comparacin ese ® 0 para x® .
Apenas utilizar esta desigualdad que ve n de antemano l ha forzado a nosotros para utilizar [ bn ] 1.
13) demuestra eso y es el Sup del successione 
naturalmente para n ® con n \ {0}.
Es necesario demostrar que la sucesina n es convergente, eso que sucede para cada monotona limitado de la sucesin y, demostraremos por lo tanto esoa n es crescent y limitado.
a n que es crescent se demuestra verificando que el Relazioneshipa n /a n -1 es mayor de 1 que se obtenga que trae detrs numerating a una forma del tipo (1 h)n y por lo tanto disuguagliando con Bernoulli. Resultado obtenido es vlido para n 2 en para cunto es solamente el error n = 1 lgico alcanzado 01 .
a n
es limitado es anlogo demostrada en una sucesin 
y verificar que Relazioneship bn / bn -1 sea
ms pequeo de 1 que se obtenga que trae detrs el numerador a uno
forma de tipo (1 h)n y por lo
tanto disuguagliando con Bernoulli.
Puede por lo tanto ser afirmado quea n est abarcado entre 0 y bn que de los estiramientos del resto al mismo lmite
en hecho tenga eso si 
Dar un valor a n que un intervalo dado de los valores asumidos se tiene dan y de bn en el cual se abarque y.
14) demuestra que est tambin 
por lo tanto no solamente para n \{0}
15) una sucesin limitada a los valores en " tiene un sottosuccessione convergente.
2 casos pueden ser verificados:
a) un elemento aparece las pocas infinitas y por lo tanto el sottosuccessione bn converge a a
b) la imagen de la sucesin es una totalidad
infinita (en cunto contiene la sucesin varios valores de los
infinites) y limitado (en cunto es limitada la sucesin) por lo
tanto para el teorema de Bolzano-Weierstass admite por lo menos un
punto de acumulacin l ".
Cada alrededor de l un sottosuccessione contiene los valores de
los infinites de la PU de la sucesin por lo tanto para crear que los
estiramientos a l, en detalle son el intorni 
que
para n® Un®l
el sottosuccessione es "n que elige ganada que el elemento de la sucesina n vuelve a entrar en Un , de tal manera crea un sottosuccessione convergente que comienza de una sucesin que podra no sea l.
16) una sucesin fundamental es limitada.
Una sucesin es fundamental si " y existe > 0 una N tales que 2 tomados cualesquiera mayores elementos n y m de N en el dominio de la sucesin se tiene eso | a n -a m | < y. Para demostrarla que tal sucesin es limitada es necesaria llevar a cabo la cuenta que para la n abarcada entre 0 y N existe un mximo M0 para m asumi que los valores dana n en cunto constituyen un sottoinsieme terminado de "n. Para n la N en lugar de otro puede ser maggiorare |a n | con Cauchy-Schwarz en hecho se tiene
|a n| = | (a n - aN)a N | | (a n -a N) | | a N | por lo tanto eligiendo m = N y arbitrariamente colocando y = 1 obtiene eso para cada n N que es che tenido |a n | 1 |a N| = M1 , despus de que todos por lo tantoa n sean limitados del mximo entre M0 y M1 .
17) criterio de Cauchy.
Descripcin: una sucesin a los valores verdaderos es convergente > es fundamental
Demuestre que una sucesin es medios fundamentales de demostrar que " y existe > 0 una N tales que llevado 2 cualesquiera mayores elementos n y m de N en el dominio de la sucesin se tiene eso | a n -a m | < y. Para hacer que uno ensambla y desfalca l ante el interior del mdulo y del disuguaglia con Cauchy-Schwarz que se obtiene eso:
| a n -a m | | a n - l | | a m - l | < y en hecho
de la convergencia de la sucesin que es 
sigue
que dado y > existir 0 una
N ms all de la cual | a n - l | < y / 2 y
substituir tal resultado en la desigualdad obtuvo con Cauchy-Schwarz
que el teorema resulta demostrado.
Occorre para aprovecharse de los 2 teoremas de siguiente:
a) una sucesin fundamental es limitada
b) una sucesin limitada a los valores en " posee siempre un sottosuccessionea la convergentedel kn a l.
Dimostriamo la convergenciaa n que es sa | a n - l | y aprovechndose del hecho queal kn converge a l, por lo tanto agregamos y desfalcamosal kn en el mdulo y aplicando la desigualdad triangular, se obtiene
| a n - l | | a n -al kn | | al kn - l | y el miembro de Il 2 es ms pequeo y en de cada cunto para n N1 ser tenida eso
| a Kn - l | < y / 2 mientras que para la definicin de la sucesin fundamental est |a n -a m| < y / 2 para n, m N2 y colocar
m = kn se tiene eso |a n -al kn | < y / 2 para n > N 2 .
Con el acuerdo
44) K es K "n entonces K es acuerdo > es cerrada y limitada
K compacta implica que cada sucesin a los valores en K tiene un sottosuccessione que los estiramientos a x K por lo tanto K estn cerrados en cunto contiene sus jefes de la acumulacin. El limitatezza de K se demuestra para la absurdidad que afirma que si hubiera una sucesin no limitada que estira a , cada su sottosuccessione tendra lmite y por lo tanto no es verdad que cada sottosuccessione estira a un elemento x K y por lo tanto no nos encontraramos en un acuerdo.
* K limitada implica que cada sucesina K a los valores en K es limitada
* Cada sucesin limitada posee un sottosuccessione convergente a un elemento l "n , tal elemento l se pica de la acumulacin para K y por lo tanto o es interno picado o se pica de frontera, y K cerrada siccome desea decir que contenga sea los puntos internos que los puntos de la frontera, alcanzan alguno que K contenga tambin l y despus de que todos lo que hemos intentado que K es compacta, que es que cada sucesin a los valores en K tiene un sottosuccessione que estire a lK.