Definiciones
Elementos de la base
1) Insieme:
Coleccin (clase, familia) de los elementos dichos de los objetos de junto.
2) subconjunto:
A l est el sottoinsieme de B si B contiene todos los elementos de a pero no contiene todos los elementos de B.
3) subconjunto c:
Un sottoinsieme es justa si es un sottoinsieme no vaco.
4) ordinata del apoyo:
Bosquejo de un apoyo constituido de un elemento con de c$r-at y de un elemento de la totalidad de B en la orden.
5) totalidad producida cartesiano a x B:
Es la totalidad formada de todos los apoyos ordenados cona A e bB.
6) relacin:
Es (una afirmacin que puede ser verdad o falsa) r(x binario predicado, y) con xX y yY
7) caracterstica del riflessivity:
a a
8) caracterstica del simmetria:
" x, y x SE x " y y " x
9) caracterstica del antisimmetria:
" x, y x SE x y ^ y x entonces y = x
10) caracterstica de la transitividad:
" x, y, z x SE x allora x z de y ^ y z
11) totale que ordena:
Se tiene el total pedir si estn llevados sin embargo 2 elementos x y y son el oppure y x del ossia x y del confrontabili.
12) Maggiorante:
Un maggiorante del elemento k X de a si es dicho
a) " a l se tiene que k l es confrontabile con a
b) " a l se tiene que a k
13) Minorante:
Un minorante del elemento k X de a si es dicho
a) " a l se tiene que k l es confrontabile con a
b) " a l se tiene que a k
14) Massimo:
Es un maggiorante a el cual pertenece con a
15) Minimo:
Es un minorante a el cual pertenece con a
16) superiore extremo dicho de Sup A:
Es el ms pequeo del maggioranti de a.
17) inferiore extremo dicho de los Inf A:
l es el ms grande del minoranti de a.
Funciones
18) Funzione:
Es un univoca de la correspondencia de X en Y que sea asociados a cada elemento X un solo elemento Y
19) Successione:
Es una funcin que tiene como el dominio
20) iniettiva de la funcin:
Es una funcin para la cual a un solo elemento de la imagen un solo elemento del dominio corresponde.
21) suriettiva de la funcin:
Es una funcin que tiene como imagen todo el codominio.
22) biiettiva de la funcin:
Es una funcin que es es el iniettiva que suriettiva.
23) totalidad numerabile:
Es una totalidad con la cual puede ser puesto en biunivoca de la correspondencia .
24) crescente de la funcin:
Un Relazioneship es tener funcin los aumenta 0
25) decrescente de la funcin:
Un Relazioneship es tener funcin los aumenta 0
26) pari de la funcin:
Es una funcin para la cual f(x) = f(-x)
27) dispari de la funcin:
Es una funcin para la cual f(-x) = - f(x)
28) gf:
Significa aplicar la funcin g a la funcin f (x)
29) triangolare de la desigualdad:
|x1 x2| |x1| |x2|
30) desigualdad de jvenes:
2|xy| y x2 y2/ y
31) desigualdad de Cauchy - Schwarz:
2|xy| x2 y2
Espacio vectorial "n
32) scalare del producto: " x, y "n , 
33) euclidea de la norma: " x
"n ,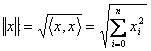 
34) Distancia Euclidiana: " x, y
"n , 
35) un definita de la funcin en un espacio vectorial verdadero X viene norma definida si goza el seguir de la caracterstica 3:
a) " x X, ||x|| 0 e ||x|| = 0 > x = 0
b) " xX, " y" ||lx|| = |l|*||x||
c) " x, y X ||x y|| ||x|| ||y||
36) un definita de la funcin en uno con X viene distancia definida si goza el seguir de la caracterstica 3:
a) " x, y X, d(x, y) 0 y d(x, y) = 0 > x = y
b) " x,yX, d(x, y) = d(y, x)
c) " x, y, d(x de z X, y) d(x, z) d(z, y)
37) distancia discreta:
si ~ de x = de yd (x,y) = 0
si ~ de x yd (x,y) = 1
38) d*(x, y):
mximo{|x1 - y1| , |x2 - y2|}
39) d*(x,y):
|x1 - y1| |x2 - y2|
Topologa
40) Intorno:
Los datos x "n y y " , son dichos alrededor de esfrico del centro x y la viga y la totalidad By(x): = { y "n : d(x, y) < y}
41) Sfera:
Los datos x "n y y " , dicen la esfera del centro x y la viga y la totalidad Sy(x): = { y "n : d(x, y) = y}
42) es X a la totalidad, porque cada xX uno es familia tenida del intorni con la caracterstica siguiente:
a) x cada U(x) para x X.
b) Si U1(x) y 2U(x) es el intorni 2 de x su interseccin contenga por lo menos uno alrededor de x.
c) si existey U(x) alrededor un U(y) contenido de y en U(x)
d) si x y existe un disgiunti U(x) de x alrededor y uno alrededor de U(y) de y: U(x) U(y) = 0
43) R* :
El refrn extenso de R es R* : = " {-} { }
44) R :
R que dice el punto es R. : = " {}
45) punto interno:
Un punto x "n adentro junto es dicho y si existe su contenido totalmente alrededor adentro y
46) describe el insieme 
Es la totalidad constituida de los solos puntos internos de y.
47) punto externo:
Un punto x "n afuera junto es dicho y si es interno la complementaria de y.
48) punto de la frontera:
Un punto x "n una dice de frontera si no es interno de externo a y.
49) describe el insieme y:
Es la totalidad constituida de los solos puntos de la frontera de y.
50) punto de la acumulacin:
Un punto x "n una dice de la acumulacin para y si cada alrededor de x contiene un punto y vario de x.
51) describe el insieme la E ':
Es la totalidad constituida de los solos puntos de la acumulacin de y.
52) punto aislado:
Un punto x "n es punto aislado dicho de y si xy y l no est de acumulacin para y.
53) con abierto:
Junto y "n es dicho abierto en "n si cada elemento de y es interno picado a y.
54) totalidad cerrada:
Junto y "n es cerrada dicho en "n si la complementaria est con abierto.
55) con limitado:
Junto y "n uno dice limitado en "n si un r existe tales que y se contiene adentro alrededor del origen r de la viga.
56) dimetro de una totalidad de Diam(E):
El dimetro se define con del final avanzado con de las distancias entre 2 puntos que pertenecen x y y a y.
57) el cierre de y se es
:
Es la totalidad formada de la unin y con de su frontera.
58) con el cuerpo:
Una totalidad dice y "n el segmento que combina es cuerpo dicho si para cada apoyo (x,y) los 2 puntos se contienen adentro y.
Lmites
59) funcin limitada:
Una funcin es limitada dicho adentro a X si tal existe un M eso ||f(x)|| M " xa.
60) mximo total o absoluto:
M " es mximo total o absoluto dicho de f adentro si x existe0 a tales que:
a) f(x) cada M para x a
b) f(x0) = M
61) mnimo total o absoluto:
m " es mnimo total o absoluto dicho de f adentro si x existe0 a tales que:
a) f(x) cada m para x a
b) f(x0) = m
62) punto del mnimo local y de premisas mnimas:
Un punto x0 dice de mnimo local si existe un tal U(x 0alrededor) ese f(x 0del f(x)) para cada x que pertenece a alrededor.
El punto es de mnimo local si f(x) > el f(x 0)para fuertemente cada x que pertenece a alrededor a la exclusin de x0 .
63) punto del mximo local y de premisas mximas:
Un punto x0 dice de mximo local si existe un tal U(x 0alrededor) ese f(x 0del f(x)) para cada x que pertenece a alrededor.
El punto es de mximo local si f(x) < el f(x 0)para fuertemente cada x que pertenece a alrededor a la exclusin de x0 .
64) lmite:
Si x0 "* es un punto de la acumulacin para X l "* es lmite dicho del f(x) para x ® x0 si para cada alrededor V de l uno U de x 0 talexiste alrededor de se para cada elemento x que pertenece a esto alrededor a la exclusin de x0 se tiene que el f(x) V.
Si entonces x0 " y l" pueden equivalente ser escritos: "y> 0, $d> 0 tales que " xX, 0 < |xx0| < d se tiene eso |f(x) - l | < y
65) alrededor de experto:
Es el intervalo [ x0 , x0 y)
66) punto de la acumulacin experta:
Un punto experto de la acumulacin se tiene cuando en cada alrededor experto de este punto hay por lo menos otro punto de junto.
67) lmite experto:
Si x0 "* es un punto experto de la acumulacin para X l "* es lmite experto dicho del f(x) para x ® x0 si para cada alrededor V de l uno U experto de x 0 talexiste alrededor de se para cada elemento x que pertenece a esto alrededor a la exclusin de x0 se tiene que el f(x) V.
68) punto del extremo:
Es un punto mnimo o mximo.
69) definicin del lmite de una sucesin:
> " y> 0 existe una N tales que para cada n >
N est tenida eso |a n - l |<y
70) reglas de o flautn:
a) o(3x) = o(x)
b) o(x del o(x)2) = o(x2) para x® mientras que es un o(x) para x®0
c) x2 * o(x) = o(x3)
d) o(o(x)) = o(x)
71) cuando f(x) = O(g(x))
Cuando es f(x) que el g(x) ellos es 2 infinitos o funciones infinitesimales pero su Relazioneship tiene un lmite terminado.
72) cuando g(x) del ~ del f(x)
Cuando es f(x) que el g(x) ellos es 2 infinitos o funciones infinitesimales para x ® x0 pero su Relazioneship es unitario.
73) condiciones para la asntota oblicua:
a) un lmite terminado para a x ®de Relazioneship f(x)/x se debe tener, anlogo para x® -.
b) Si el lmite terminado entonces se encuentra la asntota existe si el lmite para x® del f(x) - el hacha da detrs termin un valor de B que corresponda al anterior al origen de la asntota. En tal caso la asntota tiene ecuacin y = el hacha B.
74) condiciones para la asntota vertical:
Se tiene la asntota vertical cuando es el lmite para®xx 0 de la funcin ± es de la derecha que dan en un izquierdo lateral o solo.
75) definicin del sottosuccessione:
Una sucesin {bn} dice el sottosuccessione de la sucesin {a n} si la sucesin de cerca de aumento {k n}convalores adentro existe uno tales que bn =a Kn cada para n.
76) definicin de la sucesin fundamental:
Una sucesin {a n} a los valores verdaderos dice fundamental o de Cauchy si "yexiste > 0 una N tales que |a n-a m| <y para cada apoyo n, m > N.
77) definicin con del acuerdo para las sucesiones:
Una totalidad de K dice el acuerdo para las sucesiones si cada sucesin a los valores en K convergente tiene un sottosuccessione a un elemento de K.
Continuidad
78) definicin de la continuidad:
Una funcin es dicha contina en x0 X si uno de siguiente se verifica:
a) x0 es un punto aislado de X.
b) x0 es un punto
de la acumulacin para X y 
.
Es equivalente a la definicin del lmite pero con la advertencia a considerar tambin seale x0 que en lugar de otro para los lmites se no haga caso.
79) definicin de la discontinuidad dismissable en x0 :
Se tiene una discontinuidad dismissable en x0 al dominio si existe termin el lmite para x®x0 pero es vario del f(x0).
80) definicin de la discontinuidad de 1 especie (o del salto) en x0 :
Se tiene una discontinuidad de 1 especie en x0 al dominio si existen terminaron los lmites para x®x0 son de la derecha que dan a la izquierda pero son entre vario ellos.
81) definicin de la discontinuidad de 2 especies en x0 :
Se tiene una discontinuidad de 2 especies en x0 al dominio en el caso en el cual por lo menos uno de los 2 lmites l no existe o es infinito.
82) la definicin del uniforme de la funcin contina:
La funcin f dice que el uniforme contina si para cada y> 0 una d existe > 0 tales que para cada apoyo x,y X con ||x-y||<d se tiene eso || f(x) - f(y) || <y .
83) definicin de la funcin del lipschitziana:
La funcin f dice lipschitziana en X si es constante L que existe tal 0 uno eso || f(x) - f(y) || L ||x-y|| para cada x,y X.
84) definicin de la funcin de Holderiana:
La funcin f dice lipschitziana en X si existen de las constantes L > 0 y 0<< 1 tales que || f(x) - f(y) || L ||x-y|| para a cada x,y X. Donde ordenar de Holderianit es dicha.
85) definicin de la oscilacin de una funcin:
La oscilacin de una funcin W adentro a la lata asume los valores siguientes:
si f l no se limita adentro a
sup f - inf f si f l se limita adentro a
Derivabilit
86) ecuacin de la tangente recta al diagrama de la funcin en el punto (x0 , el f(x0)):
m(x-x 0 de y=del f(x 0))
87) definicin de la funcin derivabile:
Una funcin dice que derivabile si existe limite
terminado 
si existe tal lmite viene llamado
derivado.
88) definicin del derivado experto:
Si existe limite terminado 
viene
experto derivada llamada.
89) definicin del punto angular:
Se tiene se nota un punto angular si f l es continua enx 0 y el lmite del derivado de la derecha es vario del lmite del derivado de la izquierda, que uno de los 2 puede tambin ser infinito.
90) definicin del cuspid:
Se tiene un cuspid cuando el derivado antes de derecho y el derivado de la izquierda son antes infinites de la muestra opuesta.
91) definicin de la funcin del primitiva:
Una funcin de F dice el primitiva de f adentro si:
a) f es adentro I derivabile
b) cada F ' (x) = f(x) para x I
En la buena sustancia una el primitiva es la funcin que tengo antes de derivar y para recuperarme tngalo la necesidad a integrar.
92) definicin de la funcin convexa:
Una funcin f es cuerpo dicho en un intervalo si para cada apoyo x,yel segmento de los extremos (x, f(x)) (y, del f(y)) no tiene puntos bajo diagrama de f.
En otras palabras puede ser escrito que f l es convexa en > para cada x,yI, xy y para cada t (se tiene 0.1):
tf(y) ty de f((1-t)x ) (1-t)f(x).
93) definicin del punto del flesso:
Un punto del flesso se tiene si existe experto de x alrededor0 en el cual la funcin l sea cncava y alrededor de la izquierda en la cual la funcin l es convexa o viceversa.
Funciones ms variables
94-a) Definicin del lmite en "n por medio de los coordenadas cartesianos:
si para cada alrededor V de l uno U de x existe alrededor0 en
". n tales
que para cada x el pertenecer a esto alrededor a excepcin de x0 est tenido que el f(x)V.
94-b) Definicin del lmite en "n por medio de los coordenadas polares:
" 
uniforme con respecto a q
se es " alrededor de V de l tal $ d > 0
que " 0 < r < d y "q ha 
95) definicin del derivado direccional:
Si v son un pagador que pertenece
a
"n y la funcin jv (t) = f(x TV)
es derivabile en t=0 despus se define deriv direccional en la
direccin v de f en x 
el lmite.
96) definicin del derivado parcial:
Se define deriv el ognuna parcial de los derivados direccionales realizados en la direccin de uno de los portadores de la base cannica de acomodar vectorial del espacio.
97) cuando una funcin dice derivabile en un punto:
Cuando en ese punto los derivados parciales existen todos y por lo tanto el gradiente existe.
98) definicin de la funcin que tiene como el dominio differenziabile "en un punto:
Una funcin f es differenziabile en un punto x(a,b) si ah el o(h) para h 0 existe tal ese f(x h)=®f(x).
99) la definicin de los distingue:
Los distingue que el df(x) representa el incremento aguantado de la funcin como resultado de un incremento en el dominio y por lo tanto coincide con el df(x) = la f (x)dx del producto donde dx = xx0 .
definicin 100) de la funcin que tiene como el dominio "ndifferenziabile en un punto:
Una funcin f es differenziabile en un punto x(a,b) si existe "n tales que o(del f(x h) = del f(x) < a,h >||h||) para h®0.
101) significado de la afirmacin fC1(x)
Significa que esa f l es derivabile en X "n y todos los derivados parciales son continuos en X.
102) cul es lo distingue en segundo lugar y mientras que se indica
f(x)de d2 = < Hf (x)dx, dx >
103) escribe la expresin de los distingue de la orden k en x:
Polinomio 104) di Taylor:
Si f l es tiempos de m differenziabile en xX la funcin es polinomio dicho del sastre del grado m de f alrededor a x:
definicin 105) de la funcin convexa:
Una funcin es cuerpo dicho adentro con a abierto y cuerpo si para cada tf(x) abarcado ty del apoyo x,y f((1-t)x ) (1-t)f(y) para cada t entre 0 y 1.
106) punto crtico:
Un punto xcon al punto crtico abierto de f es dicho si f l es differenziabile en x y si f(x)del ` = 0 para cada pagador v "n .
punto 107) de la ensillada:
Un punto x0 dice de la ensillada para f si x0 es un punto crtico de f y si f(x) de la funcin - el f(x0) admite valores positivos usted y los valores negados a usted en cualquiera alrededor de x0 .
Integrales
subdivisin 108):
Una subdivisin del intervalo [ a,b ] es una totalidad terminada de los puntos abarcados en medio a y de b
109) en que una subdivisin es ms fina que una otra:
Una subdivisin es ms fina que una otra si contiene por lo menos un punto en ms.
110) s(D inferior de la suma, f):
La suma inferior a la subdivisin de D es pariente dicho 
la cantidad que es la suma de las reas de los
rectngulos cada uno de que tiene como base un intervalo de la
subdivisin y como altura, el mnimo asumi de la funcin en eso
espacia hacia fuera.
111) suma avanzada S(D, f):
La suma avanzada a la subdivisin de D es pariente dicho
la cantidad 
que es la suma de las reas de los
rectngulos cada uno de que tiene como base un intervalo de la
subdivisin y como altura, el mximo asumi de la funcin en eso
espacia hacia fuera.
112) funcin integrabile en segundo lugar Riemann:
Una funcin limitada dice integrabile segn Riemann en
el intervalo [ a,b ] si resulta que 
eso es si el
final avanzado con de las sumas inferiores es igual al final inferior
con de las sumas avanzadas.
113) amplitud de la subdivisin |D| :
La longitud de la ms grande es amplitud dicha de la subdivisin del intervallini caracteriza a usted de la subdivisin.
114) el integral suma (al Riemann):
Se tiene el ser m
el valor del lmite en un punto interno al intervalo que 
y si una funcin es integrabile segn Riemann para cada y existen > 0 subdivisiones de D unatales y
que | I(f) - s(Dy , f) | < y .
115) si la funcin integrabile de f adentro [ es un a,b ] y c[ a,b ] entonces muy la funcin integral del pariente de f se define para sealar c
cada para x[ a,b ]
116) funcin integrabile en sentido incorrecto:
Se introducen los 2 casos siguientes:
a) Una funcin f: (a,b ]® "
con" {-} a ese l es
integrabile segn Riemann " W(a,b) integrabile adentro es
sentido incorrecto dicho si existe termin el lmite 
b) Una funcin f: [ a,b)® "
con b"
{ } ese l es integrabile
segn Riemann " W(a,b) integrabile adentro es sentido incorrecto dicho si
existe termin el lmite 
.
117) funciones absolutamente integrabile en sentido incorrecto:
Una funcin definida f en un intervalo es absolutamente integrabile en sentido incorrecto si | f | l es integrabile en sentido incorrecto en el stesso del intervalo.