Variables vom Zufall abhängiges
1) variables vom Zufall abhängiges :
Entwurf einer Funktion, die er hat, während Herrschaft die S Ganzheit von Sie eines Experimentes und wie codominio mit den realen Zahlen ausfällt.
2) Funktion der kumulativen Verteilung :
Sie darf die Wahrscheinlichkeit quantitativ bestimmen, daß variable vom Zufall abhängige das X annehmen, daß die kleineren oder gleichen Werte zu Daten x bewerten Sie
3) Eigenschaft der Verteilungsfunktion :
) FX(-¥) = 0 FX( ¥) = 1
B) FX ist eine nicht abnehmende monotone Funktion, die ist wenn x1 £ x2 > FX(x1) £ FX(x2)
c), P{X>x} = 1 - FX(X)
d) ist die Verteilungsfunktion
vom destra ununterbrochen ![]()
und) P{x1 < X 2 £x } = FX(x2) - FX(x1)
f) der Sprung der Funktion der Verteilung in der Korrespondenz eines Punktes von Unstimmigkeit x0 ist der Wahrscheinlichkeit gleich, daß das variable man Wert x 0annimmt
4) variables vom Zufall abhängiges der ununterbrochenen Art :
Ein variables vom Zufall abhängiges x Sagen der ununterbrochenen Art, wenn seine Funktion der Verteilung ununterbrochen ist.
5) variables vom Zufall abhängiges der diskreten Art :
Ein variables vom Zufall abhängiges x Sagen der diskreten Art, wenn seine Funktion der Verteilung eine Funktion zu den Schritten ist.
6) variables vom Zufall abhängiges der Mischart :
Ein variables vom Zufall abhängiges x Sagen der Mischart, wenn seine Funktion der Verteilung Stapelverarbeitunglinie aber nicht zu den Schritten ist.
7) Verteilung empiricist :
Ein Verteilung empiricist ist eine Funktion zu den Schritten, welche wie Punkte der Herrschaft die Werte der Variable der vom Zufall abhängige Korrespondent zum Resultat des Tests, zu jeder von ihnen haben, die das Funktion empiricist einen Höhe Schritt 1/n verbindet.
8) Prozentanteil :
Der Prozentanteil u (oder das Prozentanteil n-esimo) von variablem vom Zufall abhängigem das X ist daß solcher Wertx u dieses P{X £ xu} = u. Der Funktion Prozentanteil ist folglich das umgekehrte der Verteilungsfunktion. In anderem zeigt der Prozentanteil mit 10 Wörtern an, daß der Wert von für den x der Bereich, dem von geht -¥ zu x subtended und von der Verteilungsfunktion bis 10% gleich ist.
9) Mittelpunkt von variablem vom Zufall abhängigem das X :
Entwurf des Prozentanteils des Wertes 0.5 und ist mit dem Buchstabem. angezeigt worden.
10) Funktion Wahrscheinlichkeit Dichte :
Die Dichte von Wahrscheinlichkeit fX(X) wird wie die Ableitung der Verteilungsfunktion
definiert ![]() .
.
11) Eigenschaft der Wahrscheinlichkeit Dichte :
) ist die Dichtefunktion (X) nicht negativesfX ³ 0
B) FX(x2) - FX(x1)
= ![]()
c) FX(X) = ![]()
d) ![]()
und) P{x1 < X £ x2 } = ![]()
12) Funktion der Masse der variablen Wahrscheinlichkeiten für vom Zufall abhängiges :
Entwurf der Funktion pk = P {X = xk}.
13) erwarteter Wert :
Variable der erwartete Wert von einem aleatoria X ist der Schwerpunkt der Dichte oder die Massen der Wahrscheinlichkeit in den ununterbrochenen Fällen oder in diskretem jeweiligem. Mit anderen Worten ist es der mittlere Wert der Verteilung.
14) fährt variabler erwarteter Wert von einem vom Zufall abhängigen fort:
![]()
15) erwarteter Wert von einem variablen vom Zufall abhängigen diskreten :
![]()
16) Eigenschaft der mittleren Statistiken :
) E[a*X ] = a*E[X ]
B) E[a*X b*Y ] = a*E[X ] b*E[Y ]
17) Abweichung :
Die vom Zufall abhängige variable Abweichung von einem X drückt ein Maß des âconcentrazioneâ? der Werte aus, die von einem variablen vom Zufall abhängigen um seinen mittleren Wert angenommen werden.
![]()
18) Shunting Linie Standard :
Es ist die Wurzel der Abweichung
![]()
19) fährt variable Abweichung von einem vom Zufall abhängigen fort:
![]()
20) Abweichung von einem variablen vom Zufall abhängigen diskreten:
![]()
21) quadratische Relation zwischen Durchschnitt und Abweichung:
![]()
22) Moment von Auftrag n von einem variablen vom Zufall abhängigen X:
mn = E[Xn]
23) zentriert Moment sie von Auftrag n von einem variablen vom Zufall abhängigen X:
![]()
24) Verschiedenheit von Chebyschev:
![]()
25) Verschiedenheit von Markov:
![]()
26) Variable statistisch Unabhängiges :
Zwei variables vom Zufall abhängiges X und Y sagt
statistisch Unabhängiges, wenn, 2 Sätze, die B von Werten von von
jeweiligem X und Y gegeben willkürlich sind und zu, es gehabt
wird ![]() .
.
27) variable vom Zufall abhängige Uniform :
Variable, die ein vom Zufall abhängiges man X fortsetzt,
sagt Uniform zwischen ![]() e,
e, ![]() wenn
seine Dichte im ungültigen Abstand und
wenn
seine Dichte im ungültigen Abstand und ![]() anderwohin
konstant ist.
anderwohin
konstant ist.
28) variables vom Zufall abhängiges Gaußsches :
Variable, die ein vom Zufall abhängiges man X fortsetzt, ist besagtes Gaußsches, wenn seine Funktion der Dichte von der Form ist
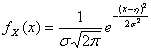
29) variabler Gaußscher Standard :
Ungültiger Entwurf von einem variablen Gaußschen mit valor Mittel und einheitlicher Abweichung.
30) Funktion der Dichte von einem variablen vom Zufall abhängigen exponentialen :
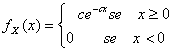
31) Funktion der Dichte von einem variablen iperexponential :
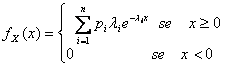
32) Funktion der Dichte von einem variablen vom Zufall abhängigen verteilten Rayleigh an zweiter Stelle :
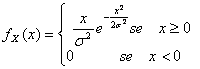
33) Funktion der Dichte von einem variablen lognormale :
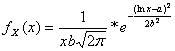
34) Funktion der Dichte von einer Variable verteilt entsprechend dem Strecke Modell :
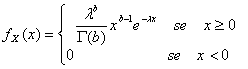
35) Funktion der Dichte von einem variablen vom Zufall abhängigen verteilt entsprechend der vorbildlichen C$abbildung :
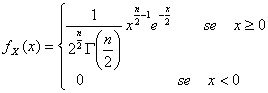
36) Funktion der Dichte von einem variablen vom Zufall abhängigen verteilt entsprechend dem Modell von Erlang :

37) Funktion der Dichte von einem variablen vom Zufall abhängigen verteilten Kursteilnehmer an zweiter Stelle :
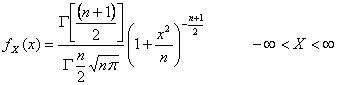
38) Funktion der Dichte von einem variablen vom Zufall abhängigen verteilt entsprechend dem K Modell :
![]()
39) Funktion der Dichte von einem variablen vom Zufall abhängigen verteilt entsprechend dem vorbildlichen Beta :

40) Funktion der Dichte von einem variablen vom Zufall abhängigen verteilt entsprechend dem Modell von Cauchy :
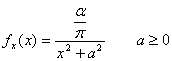
41) Funktion der Dichte von einem variablen vom Zufall abhängigen verteilt entsprechend dem binomialen Modell :
![]()
42) Funktion der Dichte von einem variablen vom Zufall abhängigen verteilt entsprechend dem geometrischen Modell :
![]()
43) variables vom Zufall abhängiges Poissoniana :
Wenn L es ein Parameter und X eins variables vom Zufall abhängiges gesamtes und positiv ist.
![]()
44) Gesetz der großen Zahlen :
In einer Reihe von n, das wiederholt wird, prüft, in
dem die Wahrscheinlichkeit des Folgens eines einzelnen Tests p, das
Verhältnis zwischen der Zahl Erfolgen k und der Zahl Ausdehnungen der
Tests n zu p wenn n ¥ gleich ® ist , ![]()
45) zentriert Theorem sie der Begrenzung für binomiale Funktionen :
In einer Reihe von n, das wiederholt wird, prüft und zeigt mit X die Zahl Erfolgen, Konstruierenvariable das vom Zufall abhängige Y an
![]()
Die Verteilung von Wahrscheinlichkeit FY(Y) ist so daß 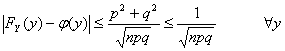
46) Funktion der Verteilung von einer variablen Funktion von vom Zufall abhängigem :
Die Funktion von Verteilung FY(Y) liefert Wahrscheinlichkeit P{Y £ y}
47) grundlegendes Theorem der Wahrscheinlichkeit Dichte :
Für einen spezifischen Wert y der Dichte fYwird (Y) da gegeben 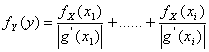
48) erwarteter Wert von einem variablen vom Zufall abhängigen Y = g(X):
![]()