Theoreme auf den Integralen
1) wenn f es ist, ist eine begrenzte Funktion undein D 1 undein D 2 2 Unterteilungen von [ a,b ]
A), wenn D1 feiner als ist, hatD 2 che s(D2,f) £ s(D1,f) £ S(D1,f) £ S(D2,f)
B) s(D1,f) £ S(D2,f)
) im Auftrag, der dieses s(D 2,f) £ s(D 1,f)
nehmen wir zeigt an, daß D1 nur einen Punkt z in mehr betreffend D 2folglich besteht ein k hat, das
zwischen 1 und n solches enthalten wird, daß der Punkt z im Abstand
(x K-1,x K)
folglichbildet nicht anderes, das
s(D 2,f schreiben)als Summe von 3 Bezeichnungen enthalten wird, von denen
das 1° es ist die minderwertige Summe bis zu zeigen Sie das
vorangeht k, 2° die Bezeichnung es das Produkt des Abstands ist (xK-1 , xK) für das Minimum auf dem gleichen Abstand und 3° die
Bezeichnung ist die minderwertige Summe von k 1 bis zu n. Das
ist 
wird dann beobachtet, das 2° die Bezeichnung
sicher ist, daß £ der
Bezeichnung, die wir betreffend würden erreichen, die minderwertige
Summe auf dem sottosuddivisione (x K-1, z,x K) in,
wieviel feineren (xdas K-1 ,
xK) und Beobachten, daß der
Anschluß dieses feineren sottosuddivisione mit 1° und 3° die
Bezeichnung nicht dieses s(D1, f sind), als analoge Demonstration es
für die vorgerückten Summen und die in einer generalisierten Weise
gebildet werden können, die es gehabt wird 
, es
ausfällt demonstrierte Teil A) des Theorems.
B) muß es demonstriert werden, daß s(D1,f) £ S(D2,f), wenn die 2 confrontabili Unterteilungen dieses immer zutreffende sind (wie werden im Teil A) des Theorems demonstriert), wenn anstatt die 2 Unterteilungen sie nicht sind, kann confrontabili eine Unterteilung D 3 danngenommen werden : = D1 ? D2 , das feiner als beide und zu erklären ist, gründete auf dem Teil A) des Theorems das
s(D1,f) £ s(D3,f) und auch S(D3,f) £ S(D2, f) und da für jede D Unterteilung es gehabtes s(D ist, f) £ S(D, f) nachdem alles conglobando diese 3 Verschiedenheiten s(D 1,f) £ S(D 2,fhat) und das Theorem wird demonstriert.
2) wenn f eine Funktion ist, die in einem Abstand [ a,b ] begrenzt wird
f ? _ "(zu, B) > " und $ ein solch dUnterteilung und von [ a,b ] dies S(Dund ,f) - s(Dund ,f) < und
wenn f? "(a,b) dann 
und für Definition von inf wird gehabt, die
genommen und > 0 zu einer $ eins D Unterteilungundzum â? so
daß S(Dundâ? ,f) < und / 2 und
eins D Unterteilungundâ ' so daß s(Dundâ ' ,f) > - und / 2. Nach aller nehmenden einer D
Unterteilungund : = Dundâ? ? Dundâ ' ihr wird das gehabt
S(Dund ,f) - s(Dund ,f) £ S(Dundâ ',f) - s(Dundâ?,f) < I(f) und / 2 - I(f) - und / 2 = und .
? hat das zweite integrabilità Riemann wenn der Unterschied zwischen dem vorgerückten Ende der Untergebensummen und dem minderwertigen Ende der vorgerückten Summen, Ausdehnungen bis 0, daß es betrachtend, daß solcher Unterschied zwischen 0 und Unterschied S(D und,f enthalten wird) - s(D und,f) < erreicht wird und das übertragenes kleines a.voluntad sein kann, das an funktioniert und.
3) wenn f es eine stetige Dauerfunktion im Abstand [ zu, b ] f ist ? "(a,b)
Es wird beobachtet, daß eine stetige
Dauerfunktion auf einem begrenzten Abstand auch auf der gleichen
folglich für jedes konstantes ununterbrochenes ist und > 0 ein d
> 0 gefunden werden kann so
daß 2 Ziel genommen worden, welches in der Herrschaft deren
gegenseitiger Abstand von d kleiner ist , gehabt werden, das ihre Bilder
minderwertig in einem Abstand zu und / Ba gefunden werden. Genug
folglich, zum von von einer D Unterteilung undvon von deren Umfang zu wählen |Dund| er ist von d kleiner und esIST in der Lage
gefunden zu werden, dem der Unterschied zwischen der Minute und dem
Maximum auf dem einzelnen ist heraus kleiner sperrt von und / Ba und infolgedessen auch der
Unterschied zwischen den vorgerückten Summen und den minderwertigen
Summen aus kleinerem von und tatsächlich sich dreht 
und an das
erinnernd wenn S(Dund ,f) - s(Dund ,f) < und dann f ? "(a,b) erzielt es einiges,
daß das Theorem demonstriert wird.
4) wenn die f Funktion, die im Abstand monoton ist, ein [ zu, b ] f ist ? "(a,b)
Die Idee der Demonstration ist, zurück zu uns zum In der LageSEIN zu holen, das zu erklären " und > 0 $ Dund , Unterteilung von [ a,b ]: S(Dund ,f) - s(Dund ,f) < und
Anlieferung folglich von 1° das Mitglied von diesem letzten und ich zeigen, daß er von und kleiner ist :
in, wieviel Annehmen der monotonen Funktion, sie zu
erhöhen gehabtes f(x)³ M dase f(x i-1)£ m Iist
in wieviel |Dund| es ist der Umfang des größten Abstands der
Unterteilung.
in, wieviel das Bild eines Funktion monotonen Halbmonds
von den 2 Werten begrenzt ist, die zu den Enden des Abstands
angenommen werden.
Die D Unterteilung folglich wählenund damit 
S(D und,f )
hat - das s(Dund das,f) < und dann das f ? "(a,b).
5) wenn f es eine Funktion ist, die im Abstand begrenzt wird [ zu, b ] und ein n° hat, das von den Punkten von discontinuità f beendet wird ? "(a,b)
Die Idee der Demonstration ist, zurück zu uns zum In der LageSEIN zu holen, das zu erklären " und > 0 $ Dund , Unterteilung von [ a,b ]: S(Dund ,f) - s(Dund ,f) < und
und folglich f? "(a,b). Wir nehmen an, daß der Unstimmigkeitpunkt zu einem Ende, als Beispiel zu und das Betrachten von von x ist?(a,b) wird es daß im Abstand [ x,b ] f gehabt ? "(x,b)das " und > ist, ist 0 $ ununterbrochene f eins D Unterteilungundâ? so, daß gehabt wird
S(Dundâ? ,f) - s(Dundâ? ,f) < und / 2. Im Abstand [
a,x ] anstatt wird es gehabt 
in wieviel für Gründlichkeit läßt die
Eigenschaft, wenn f es dann begrenzt wird, inf und sup zu und nimmt K
= sup an | f |.
, solchen Punkt x wählend das 
wie Unterteilung D folglich wählenund = Dundâ? ? {} wird es gehabt:
S(Dund ,f) -
s(Dund , f) = (M1 - m1)(x - A) S(Dundâ? ,f) - s(Dundâ? ,
wird f) 
< und folglich das
Theorem demonstriert.
6) wenn f es eine Funktion ist, die im Abstand begrenzt wird [ zu, b ] ist f entsprechend Riemann > besteht L integrierbar? " für welches "
d > 0 und >0 "so daß " D Unterteilung deren Umfang ist |D| < d, das es ausfällt |s(D,f) - L |< und .
7) wenn f und g sie integrabili Funktionen sind, die zuf bg eine integrierbare Funktion innen (a,b) ist undIST wert:
Pu², zum sich zu beobachten das
) das vorgerückte Ende der Funktion Summe ist es £ der Summe der vorgerückten Enden von den einzelnen Funktionen
B) ist das minderwertige Ende der Funktion Summe ³ der Summe der minderwertigen Enden von den einzelnen Funktionen.
c) Die Untergebensummen und die vorgerückten Summen für die gleiche Konstante kann das Integral, dem von multipliziert der Unterschied, nicht, das konstant ist.
8) wenn f und g sie integrabili Funktionen und f
£ g
sind
Es ist notwendig, zu zeigen, daß das Integral
des Funktion h(x): = g(x) - f(x) ist es ³ 0, das kommt es unten von der Tatsache, daß h(x) ³ 0 in wieviel g(x) ³f(x) folglich auch das minderwertige
Ende von h nicht negativ ist und Erinnern an die mehrfache
Verschiedenheit es gehabt wird, daß 
und das Theorem demonstriert wird.
9) wenn f und ein Funktion integrierbares
A) ist f integrierbar
B) f - er ist integrierbar
c) |f| er ist integrierbar
d) wird gehabt, das 
,
insbesondere gehabt wird 
) damit f, das er integrierbar ist, demonstriert werden muß, der " und > 0 $ Dundso daß S(Dund ,f ) - s(Dund ,f ) < und , zwecks dieses ausnutzen von der Tatsache bilden, daß f integrierbar und folglich S(D und,f ) ist - s(Dund ,f) < und . Es wird gehabt:
wo die offensichtliche Eigenschaft von f Nutzen aus zweitem der gezogen worden
ist 
.
B) Daß f - er ist wird demonstriert in der analogen Weise zu wieviel Tatsache für f integrierbar .
c) wird an das erinnernd demonstriert | f | = f f - und das Anwenden von von Theorem 120) für den Aufbau von integrabili arbeitet.
d) 
infatti f = f f -
wo ich die dreieckige Verschiedenheit angewendet
habe
im letzten habe ich dieses f und f verwendet - sie sind positive Funktionen und folglich auch ihre Integrale und che | f | = f f - .
10) wenn f und eine integrierbare Funktion innen (a,b) und c ? (a,b) dann f ist er auch auf (a,c) und an (c,b) integrierbar und fällt aus:
) zur Demonstration die f? "(a,c) und f?"(c,b)
Wenn f er auf einer D Unterteilung integrierbar ist, dann ist es zum grösseren Grund auf einer D Unterteilungund feiner, die er zu D Punkt c verbindet. Wir haben folglich die folgenden Unterteilungen: Dundâ? : = Dund ?(zu, c) e Dundâ ' : = Dund ?(c,b)
das folgende Gleichheit varrà folglich:
aber f ist entlang der Unterteilung D undfolglich integrierbar 
und wird folglich zu sein haben:
f ? "(a,c)
f ? "(c,b)
B) Demonstration das
im quanto kommt verwendete 2 Unterteilungen, die
feiner als D sindund .
Vom Rest wird es gehabt 
und folglich für die Willkür von und das Theorem wird demonstriert.
11) Theorem des Durchschnittes:
Beschreibung: Wenn f es eine integrierbare Funktion innen (a,b) ist und m ist die inf, während M das sup immer an sind (zu, B)
außerdem wenn f $ c, für das
ununterbrochenes sind 
Das Erinnern an die Verschiedenheit
e, da für Hypothese des Theorems f er integrierbares
folglich s(D ist, f) = S(D, f) wird gehabt, das 
und
Dividende für (Ba) das Theorem demonstriert wird.
Zwecks 2ª demonstrieren das Teil genug, um zu betrachten,
daß das Bild einer definierten stetigen Dauerfunktion auf einem
Abstand noch ein Abstand und folglich solches $ c das ist .
12) wenn f es eine integrierbare Funktion innen (a,b) ist und in x 0fortfährt ? (a,b) und c ? (a,b) dann die integrale Funktion
in x 0 derivabileund fällt F ' (x 0)= ist f(x0) aus.
Seiend f, das in x 0ununterbrochen ist, werden gehabt, das " und > 0 d > 0 so daß bestehen |xx0| < d e | f(x) - f(x0) | < und das ist
f(x0) -und < f(x)
< f(x0) und demonstriert und das habend,
wenn f(x) > g(x) dann 
, geschrieben werden kann:
alle für (xx 0)und ottenere teilen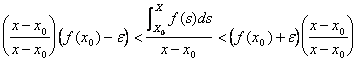 
In wieviel f(x0) und und in f(x0) -und ist konstant.
Vom Rest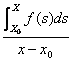 
= 
tatsächlich wird es gehabt:
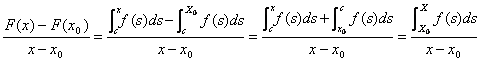
nach allen folglich 
wird ossia F '
(
x0) = f(x0 erreicht).
13) grundlegendes Theorem des integralen Kalküls:
Beschreibung: Wenn f es eine stetige Dauerfunktion auf [ zu, b ] ist
) ist die integrale Funktion auf allen [ a,b ] derivabile und seine Ableitung
ist f(x) für jedes x ? [ a,b
].
B) Wenn G ein primitiva von f [ zu, von b ]
im ist 
) folgt er einfach von der vorhergehenden Demonstration, die Beobachtung, daß stavolta das f nicht in Solenoid ein Punkt ununterbrochen ist, aber in jedem Punkt von [ a,b ] und folglich die integrale Funktion auf allen (a,b) derivabile ist und seine Ableitung ist f.
B), nehmend zu einem Punkt c nach innen zum Segment [ a,b
] kann 
scindere und siccome sein, die das Primitive
sich nur weniger als konstantes eins dieses elide mit unterscheiden -
folglich ist es auch und das Theorem folglich wird
demonstriert.
Integralangestellter von einem Parameter
14) wenn f es eine stetige Dauerfunktion in ist
[ zu, b]x[c, d ] ist 
an [ c,d ] ununterbrochen und
A) 
folglich nur geschätzt zu
werden pu², dem Integral der Begrenzung
B) Wenn f und fY auf [ zu, b]x[c, d ] J ununterbrochen ist ? Dort ([ c, d ]) und 
) ist es notwendig, das zu demonstrieren | f(Y) - f(y0)| < und zu
solchem Ziel ersetzt die Definition von f für ognuna des maggiora 2 mit dem Modul, das unter dem
Zeichen des Integrals getragen wird, das ist: 
und
das Daran erinnern, daß die Funktion f auf einem kompakten
ununterbrochen ist, hat, daß es auch folglich "und
> konstantes ununterbrochenes ist, 0 besteht d > 0 so daß für jede
Klammer y, y0 ?[ c,d ] mit |y-y0|<d wird es gehabt, daß 
das, das in
vorhergehendem das letzte Integral ersetzt wird, zurück wenn
gibt |y-y0| < d und quindi | f(Y) - f(y0)| < und .
B) Das Verlassen vom Verhältnis, welches die
Definition von diesem letzten sie des Funktion J (Y) Verwendens erhöht, wird erreicht: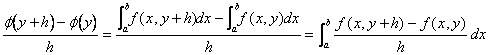 
Das Anwenden des Theorems des valor Mittels wird gehabt,
das $q ?(0.1) für das 
und hinzufügendes und unterschlagendes fY(x,y) erreicht 
.
, f ununterbrochenesY annehmend und folglich auch Uniform
fährt es fort, insofern als es auf einem kompakten beseitigt das
Erreichen definiert 
wird 
15) wenn f und fY in [ zu, b]x[c, d ] und zu ununterbrochen ist und b,
das sie 2 die Funktionen habend sind, die vor
abgeleitet werden, fährt [ c, d ] im fort die Funktion 
ununterbrochenes 1ª
an [ c,d ] abgeleitet hat und
Integrabilità in der unsachgemäßen Richtung
16-a) Kriterium des Vergleiches
Ist f,g: [ a,b)® " mit b?"* , integrabili entsprechend Riemann " W ? [ a,b), außerdem sia 0 £ f(x) £ g(x) " x?[ x0, B) , wenn g er in der unsachgemäßen Richtung innen integrierbar ist [ zu, B) f, sind in der unsachgemäßen Richtung integrierbar.
f ist er in der unsachgemäßen Richtung integrierbar,
wenn sie beendet besteht 
Das Integral 1° zum zweiten Mitglied besteht sie beendet in, wieviel die Funktion entsprechend Riemann "W integrierbar ist ?[ a,b).
Vom Integral 2° leitet man ab, daß Sein f Positiv, es
eine zunehmende monotone Funktion ist, folglich läßt es zu, daß
Begrenzung und diese Begrenzung beendet werden in, wieviel wenn f £ g auch 
und
des Restes 
in, wieviel g(x) in der unsachgemäßen
Richtung integrierbar ist.
16-b) Kriterium des Vergleiches
Ist f,g: (a,b ]® " mit zu? "* , integrabili entsprechend Riemann " W ? (a,b ], außerdem sia 0 £ f(x) £ g(x) " x?(a,x0] ist , wenn g er in der unsachgemäßen Richtung innen integrierbar ist [ zu, B) f, in der unsachgemäßen Richtung integrierbar.
17-a) Abstand nicht begrenzt
Es ist f:[a, ¥)® "endgültig Positiv für x® ¥ ED f? "[ zu,W) für ogni W > ein
A), wenn f es vom Auftrag > Infinitesimalist, ist 1 Respekt zu 1/x für® x ¥ f in der unsachgemäßen Richtung innen integrierbar [ a, ¥).
B), wenn f 1 Respekt zu 1/x vom Auftrag a£ für x ¥ ® f ist nicht integrierbar in der unsachgemäßen Richtung innen Infinitesimal ist [ a, ¥).
17-b) Funktion nicht begrenzt
Es ist f:[a, B)® " b?"endgültig Positiv für x®b - ED f? "[ zu,W) für ogni W ? (a,b )
A), wenn f es vom Auftrag < 1Respekt zu 1/(b-x) für x b endlos® ist - f ist in der unsachgemäßen Richtung innen integrierbar [ a,b).
B), wenn f 1 Respekt zu 1/(b-x) fürx b - ® ist vom Auftragzu ³ f ist nicht integrierbar in der unsachgemäßen Richtung innen endlos [ a,b).
18) wenn f es auf einem Abstand definiert wird und | f | er ist in der unsachgemäßen Richtung im integrierbar, welchesdas f in
der unsachgemäßen Richtung integrierbar ist und 
Um dieses f zu demonstrieren ist er in der unsachgemäßen Richtung genug das Theorem des Vergleich Verwendens anzuwenden integrierbar |f| zwecks dieses f und f auch herstellen - sie sind integrabili in der unsachgemäßen Richtung und folglich auch f, das f = f ist - f - .
Für die Formel anstatt wird es gehabt: 
Wo es verwendet worden ist:
) f = f - f -.
B) die dreieckige Verschiedenheit.
c) f und f- sie sind positiv, daß Funktionen, folglich auch ihre Integrale und folglich die Module unbrauchbar sind.
d) | f | = f f -.