Definitionen

Elemente der Unterseite

1) Satz:

Ansammlung (Kategorie, Familie) besagte Gegenstandelemente von zusammen.

 

2) Sottoset:

Zu ihm ist sottoset von B, wenn B alle Elemente von zu enthält, aber es nicht alle Elemente von B enthält.

 

3) Sottoset passend:

Ein sottoset ist es gerecht, wenn es ein leeres sottoset nicht ist.

 

4) Klammer ordinata:

Entwurf von einer Klammer festgesetzt von einem Element von mit c$r-at und von einem Element der B Ganzheit im Auftrag.

 

5) produzierte Ganzheit kartesisch zu x B:

Werden die Ganzheit von allen sauberen Klammern gegen zu gebildet?Ein e b?B.

 

6) Verhältnis:

Es ist gepredigtes binäres (eine Bestätigung, daß sie zutreffend oder falsch sein kann), r(x, y) mit x?X und y?Y

 

7) Eigenschaft von riflessività:

zum £ zu

 

8) Eigenschaft von Symmetrie:

" x, y ? Se X x " y ž y " x

9) Eigenschaft der Asymmetrie:

" x, y ? X Se x £ y ^ y £ x dann y = x

10) Eigenschaft von transitività:

" x, y, z ? X Se x £ y ^ y £ z allora x £ z

11) bestellengesamtmenge:

Gesamtmenge wird eine Einrichtung gehabt, wenn zu 2 Elementen x und y jedoch genommen sie confrontabili ossia x £ y oppure y £ x sind.

 

12) Maggiorante:

Ein Element k ? Maggiorante X von zu, wenn besagt ist

A), " zu?Zu ihm wird gehabt, daß k er mit zu confrontabile ist

B), " zu?Zu ihm wird daß zu £ k gehabt

 

13) Minorante:

Ein Element k ? Minorante X von zu, wenn besagt ist

A), " zu?Zu ihm wird gehabt, daß k er mit zu confrontabile ist

B), " zu?Zu ihm wird daß zu ³ k gehabt

 

14) Maximum:

Es ist ein maggiorante, dem mit gehört

 

15) Minimum:

Es ist ein minorante, dem mit gehört

 

16) Sup A besagtes extremes superiore:

Es ist vom maggioranti von zu am kleinsten.

 

17) Inf A besagtes extremes inferiore:

Er ist vom minoranti von zu am größten.

Funktionen

18) Funktion:

Es ist ein Korrespondenz univoca von X in Y, das Teilnehmer zu jedem Element ist ? X ein einzelnes Element ? Y

 

19) Reihenfolge:

Wird eine Funktion wie Herrschaft gehabt ?

 

20) Funktion iniettiva:

Es ist eine Funktion, für die einem einzelnen Element des Bildes ein einzelnes Element der Herrschaft entspricht.

 

21) Funktion suriettiva:

Ist eine Funktion, die wie Bild das ganzes codominio hat.

 

22) Funktion biiettiva:

Es ist eine Funktion, die ist iniettiva ist, das suriettiva.

 

23) Ganzheit numerabile:

Es ist eine Ganzheit, der gesetzt werden kann in Korrespondenz biunivoca mit ?.

 

24) Funktion Steigen:

Ein Verhältnis ist ein Haben von von Funktion erhöht sie ³ 0

 

25) derising Funktion:

Ein Verhältnis ist ein Haben von von Funktion erhöht sie £ 0

 

26) Funktion pari:

Es ist eine Funktion, für die f(x) = F(x)

 

27) Funktion dispari:

Es ist eine Funktion, für die F(x) = - f(x)

 

28) g°f:

Es bedeutet, die Funktion g an der Funktion f (X) anzuwenden

 

29) Verschiedenheit dreieckig:

|x₁ x₂| £ |x₁| |x₂|

 

30) Verschiedenheit der Junge:

2|xy| £ und x² y²/ und

31) Verschiedenheit von Cauchy - Schwarz:

2|xy| £ x² y²

Vectorial Raum "ⁿ

32) Produkt Scalar: " x, y ? "ⁿ ,

33) Norm euclidea: " x ? "ⁿ ,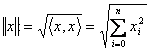

34) Euklidischer Abstand: " x, y ? "ⁿ ,

 

35) kommt eine Funktion, die auf einem realen vectorial Raum X definiert wird, definierte Norm, wenn sie genießt, der Eigenschaft 3 zu folgen:

A), " x ? X, ||x|| ³ 0 e ||x|| = 0 > x = 0

B), " x?X, " y?" ||Lx|| = |L|*||x||

c), " x, y ?X ||x y|| £ ||x|| ||y||

 

36) kommt eine Funktion, die auf einer mit X definiert wird, definierter Abstand, wenn sie genießt, der Eigenschaft 3 zu folgen:

) " x, y ? X, d(x, y) ³ 0 und d(x, y) = 0 > x = y

B), " x,y?X, d(x, y) = d(y, x)

c), " x, y, z ?D(x X, y) £ d(x, z) d(z, y)

37) diskreter Abstand:

wenn x = y ž d^~ (x,y) = 0

wenn x ¹ y ž d^~ (x,y) = 1

38) d*(x, y):

Maximum{|x₁ - y₁| , |x₂ - y₂|}

39) d_*(x,y):

|x₁ - y₁| |x₂ - y₂|

Topologie

40) herum:

Daten x ? "ⁿ und und ?" , ist um kugelförmiges von Mitte x und Lichtstrahl und Ganzheit B _und(X)besagt: = { y? "ⁿ : d(x, y) < und}

41) Bereich:

Daten x ? "ⁿ und und ?" , sagt Bereich von Mitte x und Lichtstrahl und Ganzheit S_und(X): = { y? "ⁿ : d(x, y) = und}

42) sind X eine Ganzheit, für jedes x?X man ist gehabte Familie von intorni mit der folgenden Eigenschaft:

zu) x ? Jedes U(x) für x ? X.

B) Wenn U₁(X) und ₂U(X) intorni 2 von x ž ihr Durchschnitt sind, enthalten Sie ein mindestens herum von x.

c), wenn y?U(x) ž besteht herum ein enthaltenes U(y) von y in U(x)

d), wenn x ¹ y ž ein disgiunti U(x) von x herum und von einem um U(y) von y besteht: U(x) ? U(y) = 0

 

43) R^{* :}

Umfangreicher R Saying ist R^* : = " ? {-¥} ? { ¥}

44) R ^:

R, das Punkt sagt, ist R^. : = " ? {¥}

45) innerer Punkt:

Ein Punkt x ? "ⁿ nach innen ist zusammen besagt und wenn sein vollständig enthalten herum innen besteht und

46) beschreiben den Satz

Es ist die Ganzheit, die von den einzelnen inneren Punkten von festgesetzt wird und.

 

47) externer Punkt:

Ein Punkt x ? "ⁿ draußen ist zusammen besagt und wenn es bis das ergänzende von inner ist und.

48) Punkt der Grenze:

Ein Punkt x ? "ⁿ man sagt von der Grenze, wenn es nicht von externem zu inner ist und.

49) beschreiben Satz das ¶und:

Es ist die Ganzheit, die von den einzelnen Punkten der Grenze von festgesetzt wird und.

 

50) Punkt der Ansammlung:

Ein Punkt x ? "ⁿ man sagt von der Ansammlung für und wenn jedes herum von x es einen Punkt von und verschieden von x enthält.

51) beschreiben Satz das E ':

Es ist die Ganzheit, die von den einzelnen Punkten der Ansammlung von festgesetzt wird und.

 

52) lokalisierter Punkt:

Ein Punkt x ? "ⁿ ist besagter lokalisierter Punkt von und wenn x?Und und es ist nicht von der Ansammlung für und.

53) mit geöffnet:

Zusammen und  "ⁿ ist sie geöffnet in " ⁿwenn jedes Element von besagtes und ist zu gestochenes inneres und.

54) geschlossene Ganzheit:

Zusammen und  "ⁿ ist sie in " ⁿ besagtesgeschlossenes, wenn das ergänzende man mit geöffnetem ist.

55) mit begrenztem:

Zusammen und  "ⁿ man sagt begrenztes in "^n, wenn ein r so daß besteht und innen herum vom Lichtstrahlursprung r enthalten wird.

56) Durchmesser einer Diam(E) Ganzheit:

Durchmesser wird mit vom vorgerückten Ende mit der Abstände zwischen 2 betreffenden Punkten x und y zu definiert und.

 

57) ist das Schließen von und das :

Es ist die Ganzheit, die vom Anschluß und mit seiner Grenze gebildet wird.

 

58) mit konvexem Körper:

Eine Ganzheit sagt und  "ⁿ das kombinierende Segment ist besagter konvexer Körper, wenn für jede Klammer (x,y) die 2 Punkte innen enthalten wird und.

Begrenzungen

59) begrenzte Funktion:

Eine Funktion ist innen zu  X besagtes begrenztes, wenn solches ein M das besteht ||f(x)|| £ M " x?Zu.

 

60) Gesamt- oder absolutes Maximum:

M ? " ist besagtes Gesamt- oder absolutes Maximum von f innen, wenn x ₀bestehen ? Zu so, daß:

) f(x) jedes £ M für x ? Zu

B) f(x₀) = M

 

61) Gesamt- oder absolutes Minimum:

m ? " ist besagtes Gesamt- oder absolutes Minimum von f innen, wenn x ₀bestehen ? Zu so, daß:

) f(x) jedes ³ m für x ? Zu

B) f(x₀) = m

 

62) Punkt des lokalen Minimums und der minimalen Voraussetzungen:

Ein Punkt x₀ sagt vom lokalen Minimum, wenn ein solches U(x ₀ herum)dieses f(x) ³ f(x ₀)für jedes x besteht, das herum betrifft.

Der Punkt ist vom lokalen Minimum wenn f(x) > f(x ₀)für stark jedes x, das herum Ausschluß von x ₀betrifft .

 

63) Punkt des lokalen Maximums und der maximalen Voraussetzungen:

Ein Punkt x₀ sagt vom lokalen Maximum, wenn ein solches U(x ₀ herum)dieses f(x) £ f(x ₀)für jedes x besteht, das herum betrifft.

Der Punkt ist vom lokalen Maximum wenn f(x) < f(x ₀)für stark jedes x, das herum Ausschluß von x ₀betrifft .

 

64) Begrenzung:

Wenn x₀ ? "^* es ist ein Punkt der Ansammlung für X ž L ? "^* ist besagte Begrenzung auf f(x) für x ® x_0, wenn für jedes herum V von L eins U von x _{0, das} soum das für jedes Element x betreffend dieses herum Ausschluß von x ₀besteht, gehabt wird, der f(x) ? V.

Wenn dann x₀? " und L?" Dose Äquivalent wird geschrieben: "und> 0, $d> 0 so daß " x?X, 0 < |xx₀| < d wird ihm das gehabt |f(x) - L | < und

 

65) um talentiertes:

Es ist Abstand [ x₀ , x₀ und)

 

66) Punkt der talentierten Ansammlung:

Ein talentierter Punkt der Ansammlung wird gehabt, wenn in jedem herum talentierten dieses Punktes es mindestens einen einen anderen Punkt von zusammen gibt.

 

67) talentierte Begrenzung:

Wenn x₀ ? "^* es ist ein talentierter Punkt der Ansammlung für X ž L ? "^* ist besagte talentierte Begrenzung auf f(x) für x ® x_0, wenn für jedes herum V von L eins talentiertes U vonx _{0, das} soum das für jedes Element x betreffend dieses herum Ausschluß von x ₀besteht, gehabt wird, der f(x) ? V.

 

68) Punkt des Endes:

Es ist ein minimaler oder maximaler Punkt.

 

69) Definition der Begrenzung auf eine Reihenfolge:

> " und> bestehen 0 ein N?? so, daß für jedes n > N das gehabt wird |zu_n - L |<und

 

70) Richtlinien von oder Piccoloflöte:

bis) o(3x) = o(x)

B) o(x) o(x2) = o(x2) für x® ¥, während es ein o(x) für x 0®ist

c) x² * o(x) = o(x3)

d) o(o(x)) = o(x)

 

71) wann f(x) = O(g(x))?

Wenn es f(x) ist, daß g(x) sie 2 endlos oder Infinitesimalfunktionen aber sind, ihr Verhältnis hat eine beendete Begrenzung.

 

72) wann f(x) ~ g(x)?

Wenn es f(x) ist, daß g(x) sie 2 endlos oder Infinitesimalfunktionen für x x ® ₀aber sind, ihr Verhältnis ist einheitlich.

 

73) Bedingungen für den schiefen Asymptote:

) muß eine Begrenzung, die für zum x ¥®des Verhältnisses f(x)/x beendet wird, gehabt werden, analog für x® -¥.

B) Wenn die beendete Begrenzung dann gefunden wird, besteht der Asymptote wenn die Begrenzung für x® ¥ von f(x) - Axt gibt beendete zurück einen B Wert, der dem ehemaligen dem Ursprung des Asymptote entspricht. In solchem Fall hat der Asymptote Gleichung y = Axt B.

 

74) Bedingungen für den vertikalen Asymptote:

Der vertikale Asymptote wird gehabt, wenn die Begrenzung für x®x₀ der Funktion ¥ ±ist vom Recht ist, das sie auf einem seitlichen links oder einzeln geben.

 

75) Definition von subsuccession:

Eine Reihenfolge {b_n} sagt subsuccession der Reihenfolge {zu_n} wenn nah zunehmende Reihenfolge {k _n}mitWerten innen einer besteht? so daß b_n = zu_{Kn, das} für n?jedem ist?.

 

76) Definition der grundlegenden Reihenfolge:

Eine Reihenfolge {zu_n} zu den realen Werten sagt Grundlage oder von Cauchy, wenn "und> 0 ein N bestehen?? so daß |zu_n- zu_m| <und für jede Klammer n, m > N.

77) Definition mit des Vertrages für Reihenfolgen:

Eine K Ganzheit sagt Vertrag für Reihenfolgen, wenn jede Reihenfolge zu den Werten in konvergentem K ein subsuccession zu einem Element von K hat.

Durchgang

78) Definition des Durchganges:

Eine Funktion ist fortfährt in x ₀besagt ?X wenn eins des Folgens überprüft wird:

) sindx ₀ ein lokalisierter Punkt von X.

B) sindx ₀ ein Punkt der Ansammlung für X und .

Es ist mit der Definition der Begrenzung gleichwertig, aber mit der auch zu betrachten Warnung, zeigen Sie x_0, das anstatt für die Begrenzungen ignoriert wird.

 

79) Definition der dismissable Unstimmigkeit in x₀ :

Wird einer dismissable Unstimmigkeit in x ₀gehabt ? zur Herrschaft, wenn sie beendete die Begrenzung für x x®₀besteht, aber ist von f(x ₀verschieden).

 

80) Definition der Unstimmigkeit der Sorte 1ª (oder des Sprunges) in x₀ :

Wird einer Unstimmigkeit der Sorte 1ª in x ₀gehabt ? zur Herrschaft, wenn sie bestehen, beendete die Begrenzungen für x®x₀ ist vom Recht, das sie nach links geben, aber sie zwischen verschiedenem sie sind.

 

81) Definition der Unstimmigkeit der Sorte 2ª in x₀ :

Wird einer Unstimmigkeit der Sorte 2ª in x ₀gehabt ? zur Herrschaft in dem im Fall eine mindestens der 2 Begrenzungen besteht sie nicht, oder sie ist endlos.

 

82) fährt Definition der Funktion Uniform fort:

Die Funktion f sagt, daß Uniform fortfährt, wenn für jedes und> 0 ein d > 0 so daß für jede Klammer x,y besteht ?X mit ||x-y||<d wird ihr das gehabt || f(x) - f(y) || <und .

 

83) Definition der lipschitziana Funktion:

Die Funktion f sagt lipschitziana in X, wenn konstant L, das solches ³ 0 eins das besteht || f(x) - f(y) || £ L ||x-y|| für jedes x,y ? X.

 

84) Definition der Holderiana Funktion:

Die Funktion f sagt lipschitziana in X, wenn sie von den Konstanten L > 0 und 0<<1 so daß bestehen || f(x) - f(y) || £ L ||x-y||^zu für jedem x,y ? X. Wo man von Holderianità ist besagt bestellt.

85) Definition der Pendelbewegung von einer Funktion:

Die Pendelbewegung einer Funktion W innen zur Dose nehmen die folgenden Werte an:

¥, wenn f es innen nicht auf begrenzt wird

sup f - inf f, wenn f es innen auf begrenzt wird

Derivabilità

86) Gleichung der geraden Tangente zum Diagramm der Funktion im Punkt (x₀ , in f(x₀)):

y = f(x₀) m(x-x₀)

 

87) Definition der derivabile Funktion:

Eine Funktion sagt, daß derivabile, wenn sie das beendete limite besteht, wenn solche Begrenzung besteht, benannt abgeleitet kommt.

 

88) Definition der talentierten Ableitung:

Wenn sie das beendete limite besteht, kommt sie benanntes abgeleitetes talentiertes.

 

89) Definition des eckigen Punktes:

Ein eckiger Punkt wird, wenn f es in x ₀ ununterbrochen istund die Begrenzung auf die Ableitung vom Recht von der Begrenzung auf die Ableitung vom links verschieden ist, wird beachtet gehabt, der eins der 2 endlos auch sein kann.

 

90) cuspid Definition:

Ein cuspid wird gehabt, wenn die Ableitung vorher von rechtem und die Ableitung vorher vom links infinites des gegenüberliegenden Zeichens sind.

 

91) Definition der primitiva Funktion:

Eine F Funktion sagt primitiva von f innen, wenn:

A) ist f derivabile innen I

B), jedes F ' (X) = f(x) für x ? I

In guter Substanz eine ist primitiva die Funktion, die ich habe, bevor ich ableite und zwecks mich zurückzugewinnen ihn die Notwendigkeit haben Sie zum zu integrieren.

 

92) Definition der konvexen Funktion:

Eine Funktion f ist besagter konvexer Körper in einem Abstand wenn für jede Klammer x,y?Das Segment der Enden (x, f(x)) (y, des f(y)) hat Punkte nicht unter dem Diagramm von f.

Mit anderen Worten kann es geschrieben werden, daß f es in > für jedes x,y konvex ist?I, x¹y und für jedes t ? (0.1) wird gehabt:

f((1-t)x ty) £ (1-t)f(x) tf(y).

93) Definition des Punktes von gebogen:

Ein Punkt von gebogen wird gehabt, wenn ein talentiertes von x herum ₀besteht, in dem die Funktion es und um links konkav ist, in dem die Funktion es konvex oder viceversa ist.

Variablere Funktionen

94-a) Definition der Begrenzung in "ⁿ mittels der kartesischen Koordinaten:

wenn für jedes herum V von L eins U von x herum ₀in " besteht^{. n} so, daß für jedes x das Betreffen dieses herum mit Ausnahme von x₀ gehabt wird, das f(x)?V.

 

94-b) Definition der Begrenzung in "ⁿ mittels der polaren Koordinaten:

" Uniform betreffend ist q

das ist " um V von L solches $ d > 0, das " 0 < r < d und "q ha

95) Definition der Richtungsableitung:

Wenn v ein Payer sind, der " ⁿbetrifft und die Funktion J_V (T) = f(x Fernsehapparat) ist, derivabile in t=0 dann ableiteten Richtungs in Richtung V von f in x die Begrenzung definiert wird.

 

96) Definition der teilweisen Ableitung:

Sie wird ableitete teilweises ognuna der Richtungsableitungen definiert, die in der Richtung von einer der Fördermaschinen der kanonischen Unterseite des vectorial Raumunterbringens durchgeführt werden.

 

97) wenn eine Funktion derivabile in einem Punkt sagt:

Wenn in diesem Punkt die teilweisen Ableitungen alle bestehen und folglich besteht die Steigung.

 

98) Definition der Funktion, die wie differenzierbare Herrschaft " ineinem Punkt hat:

Eine Funktion f ist in einem Punkt x differenzierbar?(a,b) wenn ah o(h) für h 0 bis solches dieses f(x h) =f(x)®bestehen.

 

99) unterscheidet Definition von sie:

Sie unterscheidet, das sie, df(x) die Stufensprung darstellt, die von der Funktion resultierend aus einer Stufensprung in der Herrschaft ausgehalten wird und folglich mit dem Produkt df(x) = f â(x)dx in dem dx = xx ₀übereinstimmt .

 

Definition 100) der Funktion, die wie die Herrschaft " ⁿdifferenzierbarin einem Punkt hat:

Eine Funktion f ist in einem Punkt x differenzierbar?(a,b) wenn es zu besteht? "ⁿ so daß f(x h) = f(x) < a,h > o(||h||) für h®0.

101) bedeutet von der Bestätigung f?C¹(X)?

Es bedeutet, daß dieses f er in X derivabile ist? "ⁿ und alle teilweisen Ableitungen sind in X ununterbrochen.

 

102) ist was unterscheidet sie an zweiter Stelle und während es angezeigt wird?

d²f(x) = < H_f (x)dx, dx >

 

103) schreiben den Ausdruck von unterscheidet sie von Auftrag k in x:

 

104) Polynomial di Taylor:

Wenn f er die m Zeiten ist, die in x differenzierbar sind?X die Funktion ist besagtes Polynom des Schneiders Grads m von f herum zu x:

 

Definition 105) der konvexen Funktion:

Eine Funktion ist besagter konvexer Körper innen zu mit geöffnetem und konvexer Körper wenn für jedes Klammer x,y f((1-t)x ty) enthaltene £ tf(x) (1-t)f(y) für jedes t zwischen 0 und 1.

 

106) kritischer Punkt:

Ein Punkt x?Zu mit geöffnetem kritischem Punkt von f ist besagt, wenn f er in x differenzierbar ist und wenn `f(x) = 0 für jeden Payer V? "ⁿ .

 

hohlrückiges Pferd Punkt 107):

Ein Punkt x₀ sagt vom hohlrückigen Pferd für f, wenn x₀ ein kritischer Punkt von f sind und wenn Funktion f(x) - f(x₀) läßt positive Werte Sie und die Werte, die zu Ihnen in verweigert werden zu, welches herum von x₀ .

Integrale

Unterteilung 108):

Eine Unterteilung des Abstands [ a,b ] ist eine beendete Ganzheit der Punkte, die zwischen zu enthalten werden und des b

 

109) als eine Unterteilung feiner als andere ist:

Eine Unterteilung ist feiner als andere, wenn sie mindestens einen Punkt in mehr enthält.

 

110) minderwertiges Summe s(D, f):

Minderwertige Summe zur D Unterteilung ist besagtes Verwandtes die Menge, die die Summe der Bereiche der Vierecke von dem jeder wie Unterseite einen Abstand der Unterteilung und wie Höhe hat, das Minimum annahm von der Funktion in dem sperrt heraus ist.

 

111) vorgerückte Summe S(D, f):

Vorgerückte Summe zur D Unterteilung ist besagtes Verwandtes die Menge, die die Summe der Bereiche der Vierecke von dem jeder wie Unterseite einen Abstand der Unterteilung und wie Höhe hat, das Maximum annahm von der Funktion in dem sperrt heraus ist.

 

112) integrierbare Funktion an zweiter Stelle Riemann:

Eine begrenzte Funktion sagt integrierbares entsprechend Riemann im Abstand [ a,b ] wenn er ausfällt, den der ist, wenn das vorgerückte Ende mit der minderwertigen Summen dem minderwertigen Ende mit der vorgerückten Summen gleich ist.

 

113) Umfang der Unterteilung |D| :

Die Länge von größtem ist besagter Umfang der Unterteilung des intervallini kennzeichnet zu Ihnen von der Unterteilung.

 

114) summiert Integral (zum Riemann):

M sein der Wert der Begrenzung in einem inneren Punkt zum Abstand wird gehabt, der und wenn eine Funktion entsprechend Riemann ž für jedes integrierbar ist und > 0 D Unterteilung eine sobesteht _und der | I(f) - s(D_und , f) | < und .

115) wenn f integrierbare Funktion innen [ ist ein a,b ] und c?[ a,b ] dann sehr wird die integrale Funktion des f Verwandten definiert, um c zu zeigen

jedes für x?[ a,b ]

 

116) integrierbare Funktion in der unsachgemäßen Richtung:

Die 2 folgenden Fälle werden eingeführt:

) eine Funktion f: (a,b ]® " mit zu?"ã?{-das ¥}, das ist er dieses ist, entsprechend Riemann " W integrierbar?(a,b) ist innen besagte unsachgemäße Richtung integrierbar, wenn sie beendete die Begrenzung besteht

B) Eine Funktion f: [ a,b)® " mit b?"ã?{ dem ¥}, das ist er diesem ist, entsprechend Riemann " W integrierbar?(a,b) ist innen besagte unsachgemäße Richtung integrierbar, wenn sie beendete die Begrenzung besteht .

117) absolut integrierbare Funktion in der unsachgemäßen Richtung:

Eine definierte Funktion f auf einem Abstand ist in der unsachgemäßen Richtung wenn absolut integrierbar | f | er ist in der unsachgemäßen Richtung auf dem Abstand stesso integrierbar.